Question
Question: In this circuit, the value of $I_2$ is ...
In this circuit, the value of I2 is
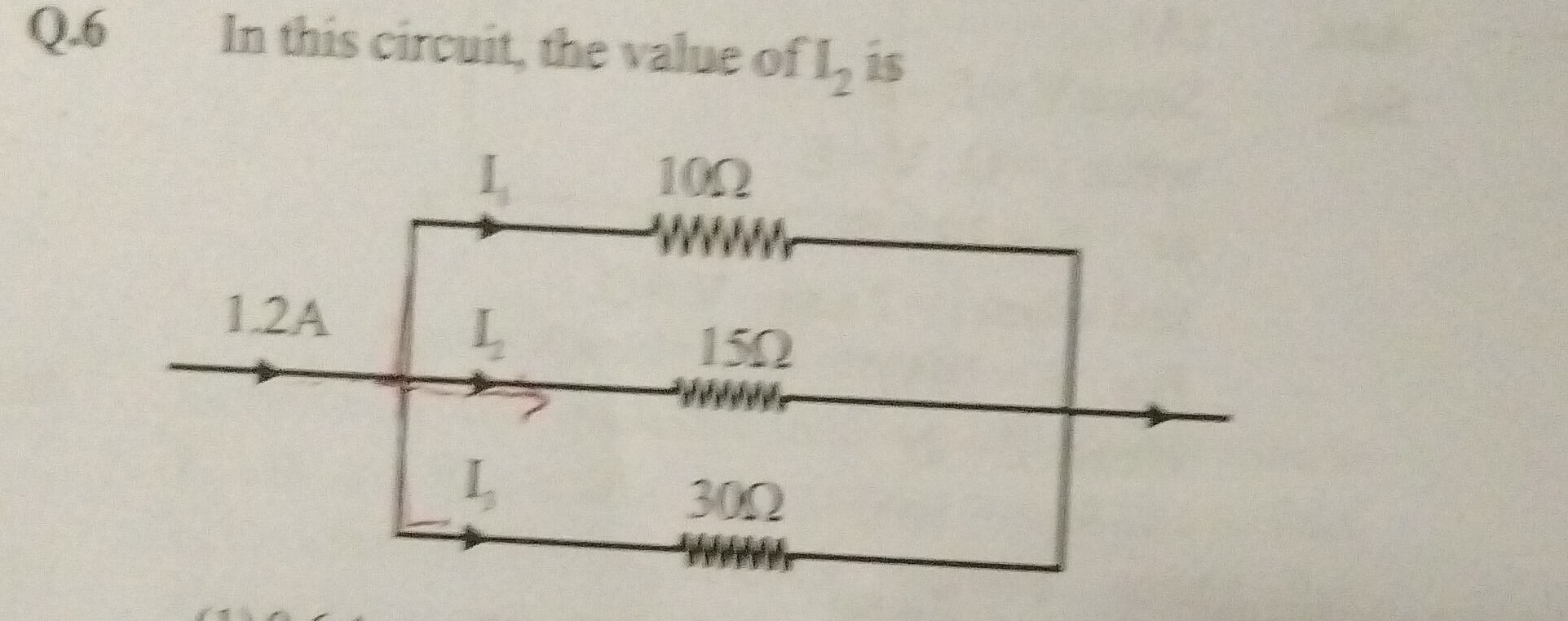
1.2A
I1 10Ω
I2 15Ω
I3 30Ω
0.4A
Solution
The circuit consists of three resistors R1=10Ω, R2=15Ω, and R3=30Ω connected in parallel. The total current entering the parallel combination is I=1.2A. We need to find the current I2 flowing through the resistor R2=15Ω.
In a parallel circuit, the voltage across each branch is the same. Let V be the voltage across the parallel combination. The current through each resistor is given by Ohm's law: I1=R1V, I2=R2V, I3=R3V
The total current is the sum of the currents in the parallel branches: I=I1+I2+I3=R1V+R2V+R3V=V(R11+R21+R31)
We can calculate the equivalent resistance Req of the parallel combination: Req1=R11+R21+R31=101+151+301
The least common multiple of 10, 15, and 30 is 30. Req1=303+302+301=303+2+1=306=51 So, Req=5Ω.
Now, we can find the voltage V across the parallel combination using Ohm's law, V=I×Req: V=1.2A×5Ω=6V.
Now we can find the current I2 through the resistor R2=15Ω: I2=R2V=15Ω6V=156A=52A=0.4A.
Alternatively, we can use the current division rule. The ratio of currents in parallel branches is inversely proportional to the ratio of their resistances. Also, the current through a branch is the total current multiplied by the ratio of the equivalent resistance of the parallel combination to the resistance of that branch, or the total current multiplied by the ratio of the conductance of that branch to the total conductance.
Using the current division rule, for a parallel circuit with total current I and branches with resistances R1,R2,R3, the current through R2 is given by: I2=I×R11+R21+R31R21=I×Req1R21=I×R2Req We calculated Req=5Ω. I2=1.2A×15Ω5Ω=1.2A×31=0.4A.
Both methods give the same result, I2=0.4A.
