Question
Question: If $y = x^{n-1} \ln x$ satisfies $x^2 \frac{d^2y}{dx^2} + a_n x \frac{dy}{dx} + b_n y = 0$ and $f(x...
If y=xn−1lnx satisfies
x2dx2d2y+anxdxdy+bny=0 and f(x)=cot−1x2−1+sec−1x2−1x+csc−1x,
then which of the following options is/are correct?
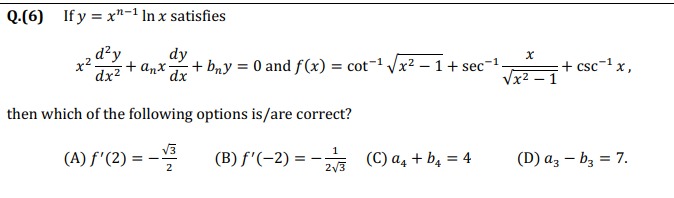
f′(2)=−23
f′(−2)=−231
a4+b4=4
a3−b3=7
(A), (B), (C)
Solution
The question has two parts. First, we need to find the coefficients an and bn of a differential equation. Second, we need to evaluate the derivative of a function involving inverse trigonometric functions.
Part 1: Differential Equation
The given differential equation is x2dx2d2y+anxdxdy+bny=0, and y=xn−1lnx. We calculate the first and second derivatives of y:
dxdy=dxd(xn−1lnx)=(n−1)xn−2lnx+xn−1⋅x1=(n−1)xn−2lnx+xn−2.
dx2d2y=dxd((n−1)xn−2lnx+xn−2)=(n−1)((n−2)xn−3lnx+xn−2⋅x1)+(n−2)xn−3=(n−1)(n−2)xn−3lnx+(n−1)xn−3+(n−2)xn−3=(n−1)(n−2)xn−3lnx+(2n−3)xn−3.
Substitute y, dxdy, and dx2d2y into the differential equation:
x2[(n−1)(n−2)xn−3lnx+(2n−3)xn−3]+anx[(n−1)xn−2lnx+xn−2]+bn[xn−1lnx]=0
Multiply by powers of x:
(n−1)(n−2)xn−1lnx+(2n−3)xn−1+an(n−1)xn−1lnx+anxn−1+bnxn−1lnx=0
Assuming x=0, divide by xn−1:
(n−1)(n−2)lnx+(2n−3)+an(n−1)lnx+an+bnlnx=0
Group terms by lnx:
[(n−1)(n−2)+an(n−1)+bn]lnx+[(2n−3)+an]=0
This equation must hold for all x in the domain of lnx (x>0). Thus, the coefficients of lnx and the constant term must be zero.
Coefficient of lnx: (n−1)(n−2)+an(n−1)+bn=0⟹n2−3n+2+an(n−1)+bn=0.
Constant term: 2n−3+an=0⟹an=3−2n.
Substitute an into the first equation:
n2−3n+2+(3−2n)(n−1)+bn=0
n2−3n+2+(3n−3−2n2+2n)+bn=0
n2−3n+2−2n2+5n−3+bn=0
−n2+2n−1+bn=0⟹bn=n2−2n+1=(n−1)2.
So, an=3−2n and bn=(n−1)2.
Check options (C) and (D):
(C) a4+b4=4. For n=4, a4=3−2(4)=−5, b4=(4−1)2=9. a4+b4=−5+9=4. Option (C) is correct.
(D) a3−b3=7. For n=3, a3=3−2(3)=−3, b3=(3−1)2=4. a3−b3=−3−4=−7. Option (D) is incorrect.
Part 2: Derivative of f(x)
The function is f(x)=cot−1x2−1+sec−1x2−1x+csc−1x. The domain of f(x) requires x2−1≥0 and ∣x∣≥1, which is ∣x∣≥1. The derivative f′(x) is defined for ∣x∣>1.
Consider x>1. Let x=secθ, where θ∈(0,π/2).
x2−1=sec2θ−1=∣tanθ∣=tanθ (since θ∈(0,π/2)).
cot−1x2−1=cot−1(tanθ)=cot−1(cot(π/2−θ))=π/2−θ=π/2−sec−1x.
x2−1x=tanθsecθ=cscθ.
sec−1x2−1x=sec−1(cscθ)=sec−1(sec(π/2−θ))=π/2−θ=π/2−sec−1x.
csc−1x=csc−1(secθ)=csc−1(csc(π/2−θ))=π/2−θ=π/2−sec−1x.
For x>1, f(x)=(π/2−sec−1x)+(π/2−sec−1x)+(π/2−sec−1x)=3π/2−3sec−1x.
f′(x)=dxd(3π/2−3sec−1x)=0−3⋅∣x∣x2−11. For x>1, ∣x∣=x, so f′(x)=−xx2−13.
Check option (A): f′(2)=−23. Since 2>1, we use f′(x)=−xx2−13.
f′(2)=−222−13=−233=−2⋅333=−23. Option (A) is correct.
Consider x<−1. Let x=secθ, where θ∈(π/2,π).
x2−1=sec2θ−1=∣tanθ∣=−tanθ (since θ∈(π/2,π)).
cot−1x2−1=cot−1(−tanθ)=cot−1(cot(π−θ))=π−θ=π−sec−1x.
x2−1x=−tanθsecθ=−cscθ.
Since x<−1, x2−1x<−1. Let y=−cscθ. Since θ∈(π/2,π), sinθ∈(0,1], cscθ∈[1,∞). So y∈(−∞,−1].
f′(x)=dxdcot−1x2−1+dxdsec−1x2−1x+dxdcsc−1x.
For ∣x∣>1:
dxdcot−1x2−1=−1+(x2−1)21⋅dxdx2−1=−1+x2−11⋅2x2−12x=−x21⋅x2−1x=−xx2−11.
dxdsec−1u=∣u∣u2−11dxdu, where u=x2−1x.
dxdu=x2−1x2−1⋅1−x⋅2x2−12x=x2−1x2−1x2−1−x2=(x2−1)x2−1−1.
∣u∣=∣x2−1x∣. u2−1=x2−1x2−1=x2−1x2−(x2−1)=x2−11. u2−1=x2−11=x2−11.
dxdsec−1x2−1x=∣x2−1x∣x2−111⋅(x2−1)x2−1−1=∣x∣⋅x2−11x2−1⋅(x2−1)x2−1−1=∣x∣x2−1⋅(x2−1)x2−1−1=−∣x∣x2−11.
dxdcsc−1x=−∣x∣x2−11.
So, for ∣x∣>1, f′(x)=−xx2−11−∣x∣x2−11−∣x∣x2−11.
If x>1, ∣x∣=x, so f′(x)=−xx2−11−xx2−11−xx2−11=−xx2−13. This matches our previous result for x>1.
If x<−1, ∣x∣=−x, so f′(x)=−xx2−11−(−x)x2−11−(−x)x2−11=−xx2−11+xx2−11+xx2−11=xx2−11.
Check option (B): f′(−2)=−231. Since −2<−1, we use f′(x)=xx2−11.
f′(−2)=−2(−2)2−11=−24−11=−231=−231. Option (B) is correct.
