Solveeit Logo
Login

Question

Question: If $a + b + c = 0$, then the value of $\frac{a^2(b+c)+b^2(c+a)+c^2(a+b)}{abc}$ is...

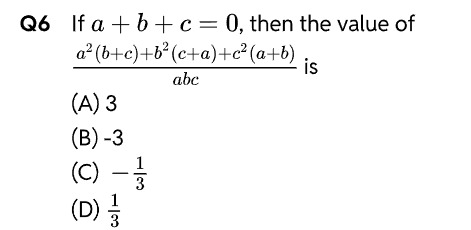
If a+b+c=0a + b + c = 0, then the value of a2(b+c)+b2(c+a)+c2(a+b)abc\frac{a^2(b+c)+b^2(c+a)+c^2(a+b)}{abc} is

A

3

B

-3

C

−13-\frac{1}{3}

D

13\frac{1}{3}

Answer

-3

Explanation

Solution

Given the condition a+b+c=0a + b + c = 0. We want to find the value of the expression a2(b+c)+b2(c+a)+c2(a+b)abc\frac{a^2(b+c)+b^2(c+a)+c^2(a+b)}{abc}.

From a+b+c=0a+b+c=0, we have: b+c=−ab+c = -a c+a=−bc+a = -b a+b=−ca+b = -c

Substitute these into the numerator: Numerator = a2(b+c)+b2(c+a)+c2(a+b)=a2(−a)+b2(−b)+c2(−c)=−a3−b3−c3=−(a3+b3+c3)a^2(b+c)+b^2(c+a)+c^2(a+b) = a^2(-a) + b^2(-b) + c^2(-c) = -a^3 - b^3 - c^3 = -(a^3 + b^3 + c^3)

Using the algebraic identity: a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ca)a^3 + b^3 + c^3 - 3abc = (a+b+c)(a^2 + b^2 + c^2 - ab - bc - ca)

Since a+b+c=0a+b+c=0, we have: a3+b3+c3−3abc=0a^3 + b^3 + c^3 - 3abc = 0 a3+b3+c3=3abca^3 + b^3 + c^3 = 3abc

Substitute this back into the numerator: Numerator = −(a3+b3+c3)=−(3abc)-(a^3 + b^3 + c^3) = -(3abc)

So the expression becomes: −(3abc)abc=−3\frac{-(3abc)}{abc} = -3, assuming abc≠0abc \neq 0.

Therefore, the value of the expression is -3.