Question
Question: Let A be a matrix such that adj (adj A) = $\begin{bmatrix} 5 & 2 & 1 \\ 3 & 1 & 0 \\ 2 & 2 & 1 \end{...
Let A be a matrix such that adj (adj A) = 532212101 then the value of det (3A−1) is
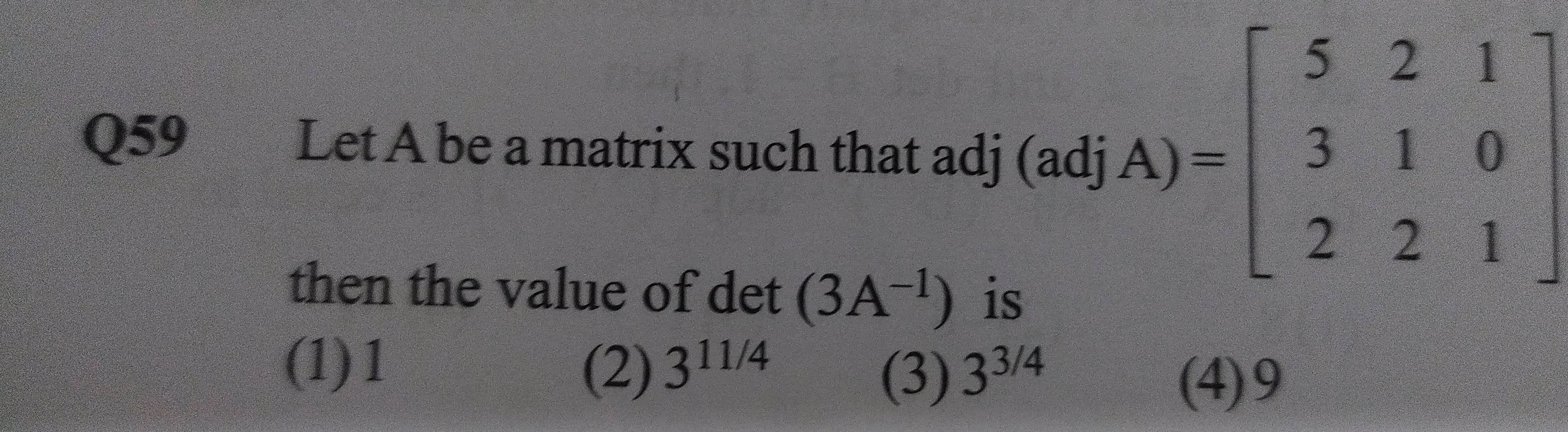
1
311/4
33/4
9
311/4
Solution
The given matrix is adj(adjA)=B=532212101. The order of the matrix A is determined by the order of adj(adjA). Since B is a 3×3 matrix, A must also be a 3×3 matrix. Let the order of A be n=3.
We need to find the value of det(3A−1). Using the property det(kA)=kndet(A), we have det(3A−1)=3ndet(A−1). For n=3, det(3A−1)=33det(A−1). Using the property det(A−1)=det(A)1, we have det(3A−1)=33det(A)1. To find the value, we need to determine det(A).
We are given adj(adjA)=B. For a square matrix A of order n≥2, we have the property adj(adjA)=(detA)n−2A. For n=3, this property becomes adj(adjA)=(detA)3−2A=(detA)A. So, we have (detA)A=B.
Taking the determinant of both sides: det((detA)A)=det(B). Using the property det(kA)=kndet(A) with k=detA and n=3: (detA)3det(A)=det(B). (detA)4=det(B).
Now, we calculate the determinant of matrix B: B=532212101 det(B)=5⋅1201−2⋅3201+1⋅3212 det(B)=5(1×1−0×2)−2(3×1−0×2)+1(3×2−1×2) det(B)=5(1)−2(3)+1(6−2) det(B)=5−6+4 det(B)=3.
Substituting the value of det(B) into the equation (detA)4=det(B): (detA)4=3. This equation implies det(A)=±31/4.
We need to find det(3A−1)=33det(A)1. If det(A)=31/4, then det(3A−1)=3331/41=33−1/4=312/4−1/4=311/4. If det(A)=−31/4, then det(3A−1)=33−31/41=−311/4.
The given options are all positive values. This suggests that either the problem assumes det(A)>0, or the context implies it. Assuming det(A)>0, we take det(A)=31/4.
Then, det(3A−1)=311/4.
Comparing this with the given options: (1) 1 (2) 311/4 (3) 33/4 (4) 9
The calculated value 311/4 matches option (2).
The final answer is 311/4.
Explanation of the solution:
- Identify the order of matrix A from the given matrix adj(adjA). Since adj(adjA) is 3×3, A is 3×3 (order n=3).
- Use the property det(kA)=kndet(A) to express det(3A−1) in terms of det(A): det(3A−1)=33det(A−1)=33/det(A).
- Use the property adj(adjA)=(detA)n−2A. For n=3, this is adj(adjA)=(detA)A.
- Take the determinant of both sides of (detA)A=adj(adjA). This gives (detA)ndet(A)=det(adj(adjA)), which simplifies to (detA)4=det(adj(adjA)).
- Calculate the determinant of the given matrix adj(adjA). The determinant is 3.
- Solve (detA)4=3 for det(A). This gives det(A)=±31/4.
- Assuming det(A)>0 (based on the positive options), take det(A)=31/4.
- Substitute the value of det(A) into the expression for det(3A−1): det(3A−1)=33/31/4=311/4.
- Match the result with the given options.
The final answer is 311/4.
