Question
Question: If $\vec{a}=\hat{i}+2\hat{j}+\hat{k}$, $\vec{b}=3(\hat{i}-\hat{j}+\hat{k})$ and $\vec{c}$ be the vec...
If a=i^+2j^+k^, b=3(i^−j^+k^) and c be the vector such that a×c=b and a⋅c=3, then a⋅((c×b)−b−c) is equal to
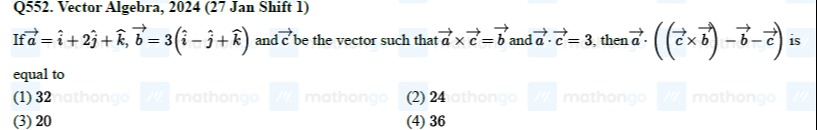
32
24
20
36
24
Solution
Given:
a=i^+2j^+k^, b=3(i^−j^+k^), a×c=b, a⋅c=3.
We need to find S=a⋅((c×b)−b−c).
Step 1: Write S as:
S=(I)a⋅(c×b)−a⋅b−a⋅c.
Since
a⋅b=a⋅(a×c)=0 (dot product of a vector with its cross product is zero),
and a⋅c=3, we get
S=a⋅(c×b)−3.
Step 2: Note that b=a×c. Then
a⋅(c×b)=a⋅(c×(a×c)).
Using the vector triple product identity:
c×(a×c)=(c⋅c)a−(c⋅a)c,
we have
a⋅[(c⋅c)a−(c⋅a)c]=(c⋅c)(a⋅a)−(c⋅a)2.
Given:
a⋅a=12+22+12=6, a⋅c=3.
Let ∣c∣2=c⋅c. Then
a⋅(c×b)=6∣c∣2−9.
Thus,
S=6∣c∣2−9−3=6∣c∣2−12.
Step 3: Find ∣c∣2 using the relation from a×c=b.
The magnitude of the cross product is:
∣a×c∣=∣a∣∣c∣sinθ,
and since b=3(i^−j^+k^),
∣b∣=312+(−1)2+12=33.
Thus,
∣a∣∣c∣sinθ=33.
Also, from the dot product:
a⋅c=∣a∣∣c∣cosθ=3.
Here, ∣a∣=6. Let ∣c∣=d. Then:
cosθ=6d3 and sinθ=1−6d29=6d26d2−9.
Substituting in the cross product magnitude:
6d⋅6d26d2−9=33.
Simplify:
6d2−9=33⟹6d2−9=27⟹6d2=36⟹d2=6.
Thus, ∣c∣2=6.
Step 4: Substitute back in S:
S=6⋅6−12=36−12=24.
Therefore, the answer is 24.
