Question

Solve for $x$: $x^2 + |x-1| = 1$

Answer 1

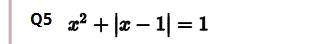
The solutions are $x = 0, 1$.

Answer 2

The given equation is $x^2 + |x-1| = 1$. To solve this equation, we consider the two cases based on the definition of the absolute value function $|x-1|$.

Case 1: $x-1 \ge 0$, which means $x \ge 1$. In this case, $|x-1| = x-1$. The equation becomes: $x^2 + (x-1) = 1$ $x^2 + x - 1 = 1$ $x^2 + x - 2 = 0$ This is a quadratic equation. We can factor it: $(x+2)(x-1) = 0$ The possible solutions are $x+2=0$ or $x-1=0$. This gives $x = -2$ or $x = 1$. We must check if these solutions satisfy the condition for this case, which is $x \ge 1$. For $x = -2$, the condition $x \ge 1$ is not satisfied (since $-2 < 1$). So, $x = -2$ is not a valid solution in this case. For $x = 1$, the condition $x \ge 1$ is satisfied (since $1 \ge 1$). So, $x = 1$ is a valid solution.

Case 2: $x-1 < 0$, which means $x < 1$. In this case, $|x-1| = -(x-1) = 1-x$. The equation becomes: $x^2 + (1-x) = 1$ $x^2 + 1 - x = 1$ $x^2 - x + 1 - 1 = 0$ $x^2 - x = 0$ This is a quadratic equation. We can factor out $x$: $x(x-1) = 0$ The possible solutions are $x=0$ or $x-1=0$. This gives $x = 0$ or $x = 1$. We must check if these solutions satisfy the condition for this case, which is $x < 1$. For $x = 0$, the condition $x < 1$ is satisfied (since $0 < 1$). So, $x = 0$ is a valid solution in this case. For $x = 1$, the condition $x < 1$ is not satisfied (since $1 \not< 1$). So, $x = 1$ is not a valid solution in this case.

Combining the valid solutions from both cases, we get $x=1$ (from Case 1) and $x=0$ (from Case 2). Thus, the solutions to the equation $x^2 + |x-1| = 1$ are $x=0$ and $x=1$.

We can verify the solutions: For $x=0$: $0^2 + |0-1| = 0 + |-1| = 0 + 1 = 1$. (Correct) For $x=1$: $1^2 + |1-1| = 1 + |0| = 1 + 0 = 1$. (Correct)

Therefore, the solutions are $x = 0, 1$.