Question

Two dice are thrown simultaneously. If at least one of the dice shows number 5, then the probability that, sum of the numbers on two dice is 9 is

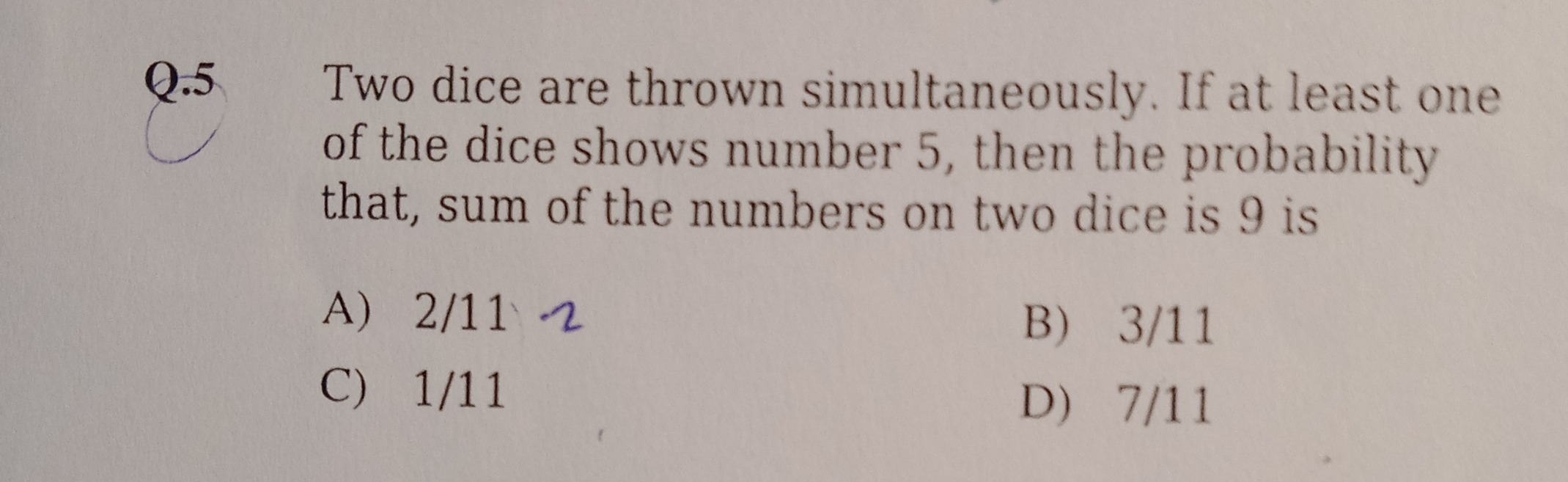
• A. 2/11
• B. 3/11
• C. 1/11
• D. 7/11

Answer 1

Answer: (A)

2/11

Answer 2

To solve this problem, we use the concept of conditional probability.

Let A be the event that the sum of the numbers on the two dice is 9.
Let B be the event that at least one of the dice shows the number 5.
We need to find the probability of event A occurring given that event B has occurred, denoted as P(A|B).

The formula for conditional probability is:

$P(A|B) = \frac{P(A \cap B)}{P(B)}$

Alternatively, this can be calculated as:

$P(A|B) = \frac{\text{Number of outcomes in } (A \cap B)}{\text{Number of outcomes in } B}$

First, let's list the total possible outcomes when two dice are thrown. The total number of outcomes is $6 \times 6 = 36$.

1. Determine the outcomes for event B (at least one die shows 5):

The outcomes where at least one die shows 5 are:

(1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 6)
(Note: (5,5) is listed only once)
The number of outcomes in B, $n(B) = 6 + 5 = 11$.

2. Determine the outcomes for event A (sum of numbers is 9):

The outcomes where the sum of the numbers is 9 are:

(3, 6), (4, 5), (5, 4), (6, 3)
The number of outcomes in A, $n(A) = 4$.

3. Determine the outcomes for the intersection of A and B ($A \cap B$) (sum is 9 AND at least one die shows 5):

From the outcomes of event A, we identify which ones also satisfy event B (at least one 5):

(4, 5) - This outcome has a sum of 9 and contains a 5.
(5, 4) - This outcome has a sum of 9 and contains a 5.

So, the outcomes in $A \cap B$ are {(4, 5), (5, 4)}.
The number of outcomes in $A \cap B$, $n(A \cap B) = 2$.

4. Calculate the conditional probability P(A|B):

Using the formula $P(A|B) = \frac{n(A \cap B)}{n(B)}$:

$P(A|B) = \frac{2}{11}$

The probability that the sum of the numbers on two dice is 9, given that at least one of the dice shows number 5, is 2/11.