Question
Question: Three concentric circles of which the biggest is $x^2 + y^2 = 1$, have their radii in A.P. If the li...
Three concentric circles of which the biggest is x2+y2=1, have their radii in A.P. If the line y=x+1 cuts all the circles in real and distinct points. The interval in which the common difference of the A.P. will lie is
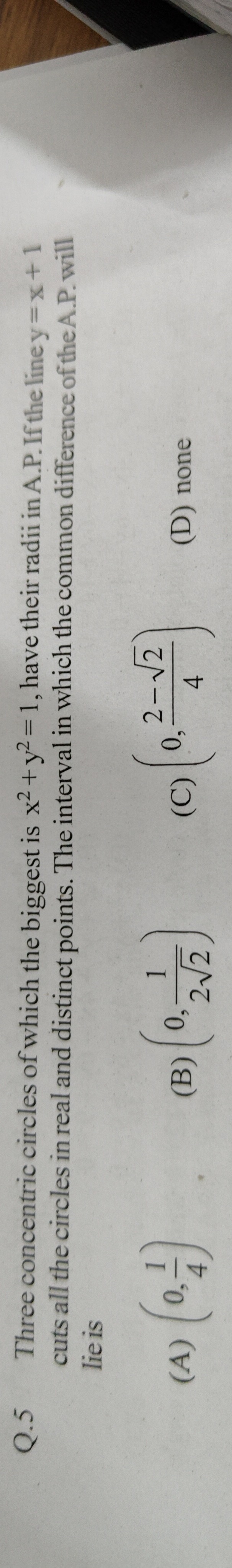
(0,41)
(0,221)
(0,42−2)
none
(0,42−2)
Solution
Let the radii of the three concentric circles be r1,r2,r3. The circles are concentric, so their center is at the origin (0,0). The largest circle is x2+y2=1, so its radius is Rmax=1. The radii are in an Arithmetic Progression (A.P.). Let the common difference be d. Since 1 is the largest radius, the radii must be in decreasing order. Let the radii be 1,1−d,1−2d. For these to be valid positive radii, we must have 1−2d>0, which implies d<1/2. For distinct radii, d=0. Since 1 is the largest radius, d must be positive. Thus, 0<d<1/2.
The equation of the line is y=x+1, which can be written as x−y+1=0. The distance p from the center of the circles (0,0) to the line is given by: p=12+(−1)2∣1(0)−1(0)+1∣=21
For the line to cut all three circles in real and distinct points, the distance p must be less than each radius: p<ri for i=1,2,3. This implies p<min(ri). The smallest radius is 1−2d. So, we must have: 21<1−2d
Rearranging this inequality to solve for d: 2d<1−21 d<21(1−21)
We also have the condition 0<d<1/2. Let's evaluate the upper bound: 21(1−21)=21(22−1)=222−1 To rationalize the denominator, multiply by 22: 222(2−1)2=42−2
Since 42−2<21, the condition d<1/2 is automatically satisfied. Therefore, the interval for the common difference d is 0<d<42−2.
