Question
Question: The value of $\lim_{x \to \infty} (\frac{2x-1}{2x+3})^{\frac{x+1}{2}}$ is:...
The value of limx→∞(2x+32x−1)2x+1 is:
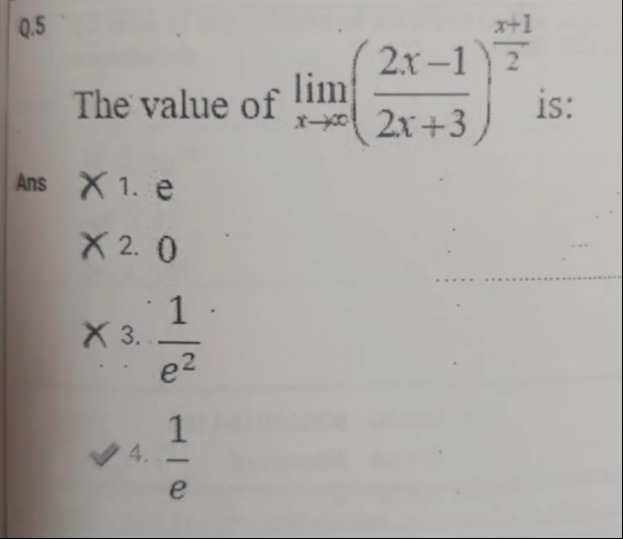
e
0
e21
e1
e1
Solution
The limit is of the form limx→∞[f(x)]g(x), where f(x)=2x+32x−1 and g(x)=2x+1. As x→∞, limx→∞f(x)=limx→∞2x+32x−1=limx→∞2+3/x2−1/x=22=1. As x→∞, limx→∞g(x)=limx→∞2x+1=∞. This is the 1∞ indeterminate form.
The limit can be evaluated using the formula: limx→∞[f(x)]g(x)=elimx→∞g(x)[f(x)−1]
First, calculate f(x)−1: f(x)−1=2x+32x−1−1=2x+32x−1−(2x+3)=2x+32x−1−2x−3=2x+3−4.
Next, calculate the limit of the exponent, L=limx→∞g(x)[f(x)−1]: L=limx→∞(2x+1)(2x+3−4) L=limx→∞2(2x+3)−4(x+1) L=limx→∞2x+3−2(x+1) L=limx→∞2x+3−2x−2
To evaluate this limit as x→∞, divide the numerator and the denominator by the highest power of x in the denominator, which is x: L=limx→∞x2x+x3x−2x−x2 L=limx→∞2+3/x−2−2/x As x→∞, 2/x→0 and 3/x→0. L=2+0−2−0=2−2=−1.
The value of the original limit is eL=e−1. e−1=e1.
The final answer is e1.
