Question

The determinant

$\begin{vmatrix} -2a & a+b & c+a \\ a+b & -2b & b+c \\ c+a & b+c & -2c \end{vmatrix}$ is divisible

by

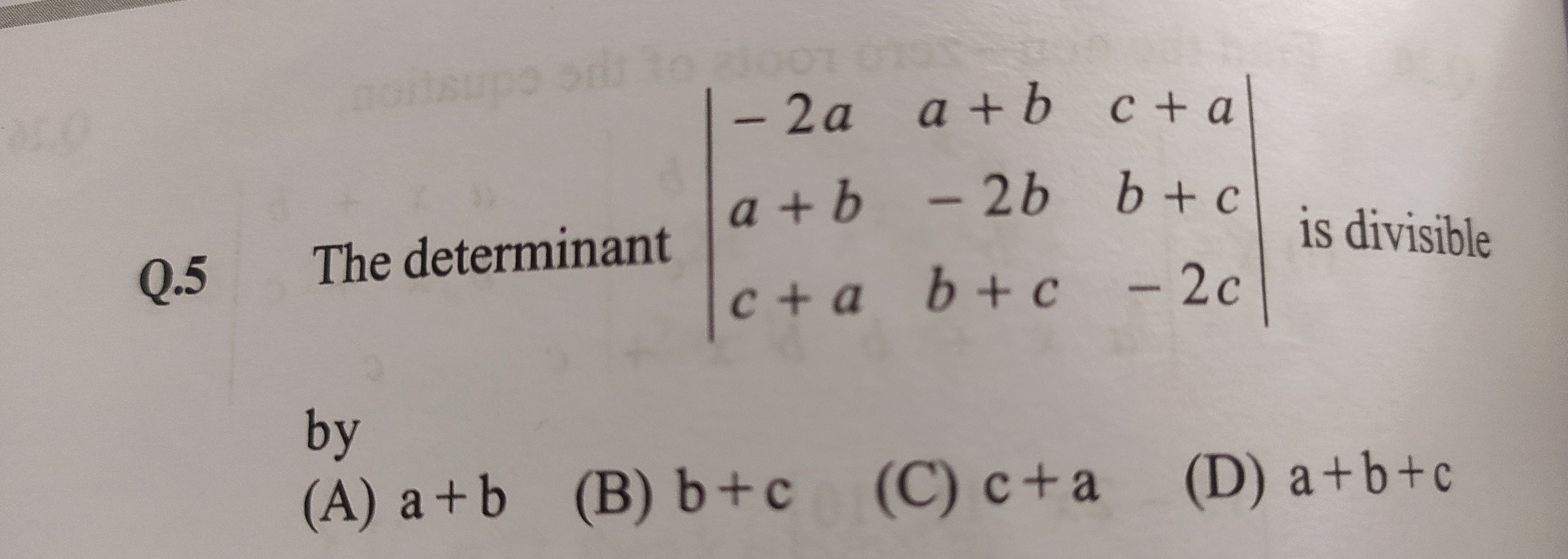
• A. a+b
• B. b+c
• C. c+a
• D. a+b+c

Answer 1

Answer: (A), (B), (C)

(A), (B), (C)

Answer 2

We are given the determinant

$$D = \begin{vmatrix} -2a & a+b & c+a \\ a+b & -2b & b+c \\ c+a & b+c & -2c \end{vmatrix}.$$

Step 1. Check the factor $(a+b)$:

Set $a+b=0$ (i.e. $a=-b$). For any value of $c$, the entries in the first two rows become related. For example, choose $a=-1$, $b=1$ (so $a+b=0$), and any $c$ (say $c=2$). The determinant then becomes

$$D=\begin{vmatrix} -2(-1)=2 & 0 & c+a=2+(-1)=1 \\ 0 & -2(1)=-2 & b+c=1+2=3 \\ c+a=1 & b+c=3 & -2c=-4 \end{vmatrix}.$$

A quick calculation shows $D=0$. Hence, $(a+b)$ is a factor.

Step 2. Check the factor $(b+c)$:

Set $b+c=0$ (i.e. $c=-b$). For example, choose $b=-1$, $c=1$, and let $a=2$. Then

$$D=\begin{vmatrix} -2(2)=-4 & a+b=2+(-1)=1 & c+a=1+2=3 \\ a+b=1 & -2(-1)=2 & 0\ (\text{since }b+c=0) \\ c+a=3 & 0 & -2(1)=-2 \end{vmatrix}.$$

The determinant computes to 0, so $(b+c)$ is a factor.

Step 3. Check the factor $(c+a)$:

Set $c+a=0$ (i.e. $c=-a$). For instance, choose $a=1$, $c=-1$ and $b=2$. Then

$$D=\begin{vmatrix} -2(1)=-2 & a+b=1+2=3 & 0 \\ a+b=3 & -2(2)=-4 & b+c=2+(-1)=1 \\ 0 & b+c=1 & -2(-1)=2 \end{vmatrix}.$$

Again, a quick calculation shows $D=0$. Hence, $(c+a)$ is a factor.

Step 4. Check the factor $(a+b+c)$:

If we set $a+b+c=0,$ then the determinant should be 0 if $(a+b+c)$ is a factor. However, testing with $a=1$, $b=2$, and $c=-3$ (so $1+2-3=0$), we get

$$D=\begin{vmatrix} -2 & 3 & -2 \\ 3 & -4 & -1 \\ -2 & -1 & 6 \end{vmatrix}.$$

A careful computation shows $D\ne 0$ (in fact, $D=24$ in this case). Thus, $(a+b+c)$ is not a factor.

---

The determinant is divisible by $(a+b)$, $(b+c)$, and $(c+a)$.