Question
Question: Number of complex numbers satisfying the relation $|z + \overline{z}| + |z - \overline{z}| = 2$ and ...
Number of complex numbers satisfying the relation ∣z+z∣+∣z−z∣=2 and ∣z+i∣+∣z−i∣=2, is
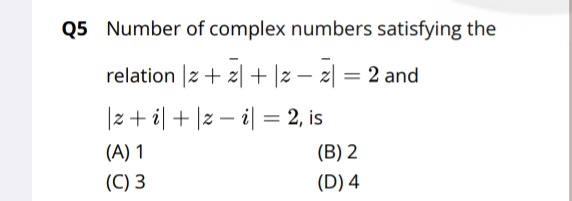
1
2
3
4
2
Solution
Let z=x+iy, where x and y are real numbers. Then z=x−iy.
We are given two conditions:
- ∣z+z∣+∣z−z∣=2
- ∣z+i∣+∣z−i∣=2
Let's analyze the first condition: z+z=(x+iy)+(x−iy)=2x z−z=(x+iy)−(x−iy)=2iy
Substitute these into the first condition: ∣2x∣+∣2iy∣=2 2∣x∣+2∣i∣∣y∣=2 Since ∣i∣=1: 2∣x∣+2∣y∣=2 Dividing by 2, we get: ∣x∣+∣y∣=1
This equation represents a square in the complex plane (or xy-plane) with vertices at (1,0), (0,1), (−1,0), and (0,−1).
Now let's analyze the second condition: ∣z+i∣+∣z−i∣=2 This equation is of the form ∣z−F1∣+∣z−F2∣=2a, which describes the locus of a point z such that the sum of its distances from two fixed points (foci F1 and F2) is a constant 2a. In this case, the foci are F1=−i and F2=i. The distance between the foci is 2c=∣i−(−i)∣=∣2i∣=2. The given sum of distances is 2a=2.
Since 2a=2c, the ellipse degenerates into the line segment connecting the two foci. Therefore, z must lie on the line segment connecting −i and i. This means z must be a purely imaginary number z=iy, where the imaginary part y is between −1 and 1 (inclusive). So, x=0 and −1≤y≤1.
Now we need to find the complex numbers z=x+iy that satisfy both conditions. From the second condition, we know x=0. Substitute x=0 into the first condition: ∣0∣+∣y∣=1 ∣y∣=1 This implies y=1 or y=−1.
Both y=1 and y=−1 satisfy the range −1≤y≤1 obtained from the second condition. Thus, the possible values for z are:
- x=0,y=1⟹z=0+i(1)=i
- x=0,y=−1⟹z=0+i(−1)=−i
Let's verify these solutions:
For z=i:
- ∣i+i∣+∣i−i∣=∣i−i∣+∣i−(−i)∣=∣0∣+∣2i∣=0+2=2. (Satisfied)
- ∣i+i∣+∣i−i∣=∣2i∣+∣0∣=2+0=2. (Satisfied)
For z=−i:
- ∣−i+−i∣+∣−i−−i∣=∣−i+i∣+∣−i−(−i)∣=∣0∣+∣−2i∣=0+2=2. (Satisfied)
- ∣−i+i∣+∣−i−i∣=∣0∣+∣−2i∣=0+2=2. (Satisfied)
Both z=i and z=−i satisfy both given conditions. Therefore, there are 2 complex numbers satisfying the given relations.
