Question

Let $\vec{a} = \alpha \hat{i} + 3\hat{j} - \hat{k}$, $\vec{b} = 3\hat{i} - \beta\hat{j} + 4\hat{k}$ and $\vec{c} = \hat{i} + 2\hat{j} - 2\hat{k}$ where $\alpha, \beta \in R$ be three vectors. If the projection of $\vec{a}$ on $\vec{c}$ is 5 units and $\vec{b} \times \vec{c} = -6\hat{i} + 10\hat{j} + 7\hat{k}$ then $\alpha + \beta =$

Answer 1

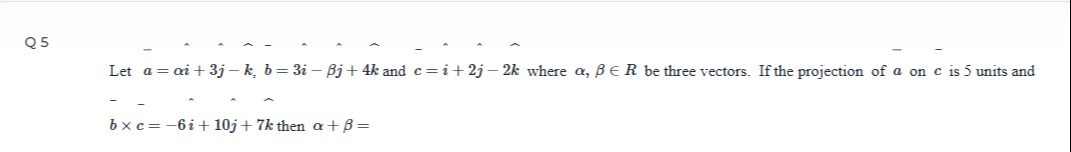
8

Answer 2

1. Calculate $\alpha$ using the projection condition: The projection of vector $\vec{a}$ on vector $\vec{c}$ is given by $\frac{\vec{a} \cdot \vec{c}}{|\vec{c}|}$. Given $\vec{a} = \alpha \hat{i} + 3\hat{j} - \hat{k}$ and $\vec{c} = \hat{i} + 2\hat{j} - 2\hat{k}$. The dot product $\vec{a} \cdot \vec{c}$ is: $\vec{a} \cdot \vec{c} = (\alpha)(1) + (3)(2) + (-1)(-2) = \alpha + 6 + 2 = \alpha + 8$ The magnitude of $\vec{c}$ is: $|\vec{c}| = \sqrt{1^2 + 2^2 + (-2)^2} = \sqrt{1 + 4 + 4} = \sqrt{9} = 3$ The projection is given as 5 units: $\frac{\alpha + 8}{3} = 5$ $\alpha + 8 = 15$ $\alpha = 7$

2. Calculate $\beta$ using the cross product condition: Given $\vec{b} = 3\hat{i} - \beta\hat{j} + 4\hat{k}$ and $\vec{c} = \hat{i} + 2\hat{j} - 2\hat{k}$. The cross product $\vec{b} \times \vec{c}$ is calculated as: $\vec{b} \times \vec{c} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -\beta & 4 \\ 1 & 2 & -2 \end{vmatrix}$ $\vec{b} \times \vec{c} = \hat{i}((-\beta)(-2) - (4)(2)) - \hat{j}((3)(-2) - (4)(1)) + \hat{k}((3)(2) - (-\beta)(1))$ $\vec{b} \times \vec{c} = \hat{i}(2\beta - 8) - \hat{j}(-6 - 4) + \hat{k}(6 + \beta)$ $\vec{b} \times \vec{c} = (2\beta - 8)\hat{i} + 10\hat{j} + (6 + \beta)\hat{k}$ We are given that $\vec{b} \times \vec{c} = -6\hat{i} + 10\hat{j} + 7\hat{k}$. Equating the components: For the $\hat{i}$ component: $2\beta - 8 = -6 \implies 2\beta = 2 \implies \beta = 1$ For the $\hat{k}$ component: $6 + \beta = 7 \implies \beta = 1$ The $\hat{j}$ component $10 = 10$ is consistent. Thus, $\beta = 1$.

3. Calculate $\alpha + \beta$: With $\alpha = 7$ and $\beta = 1$: $\alpha + \beta = 7 + 1 = 8$