Question
Question: $\int \frac{dx}{1+e^x}$...
∫1+exdx
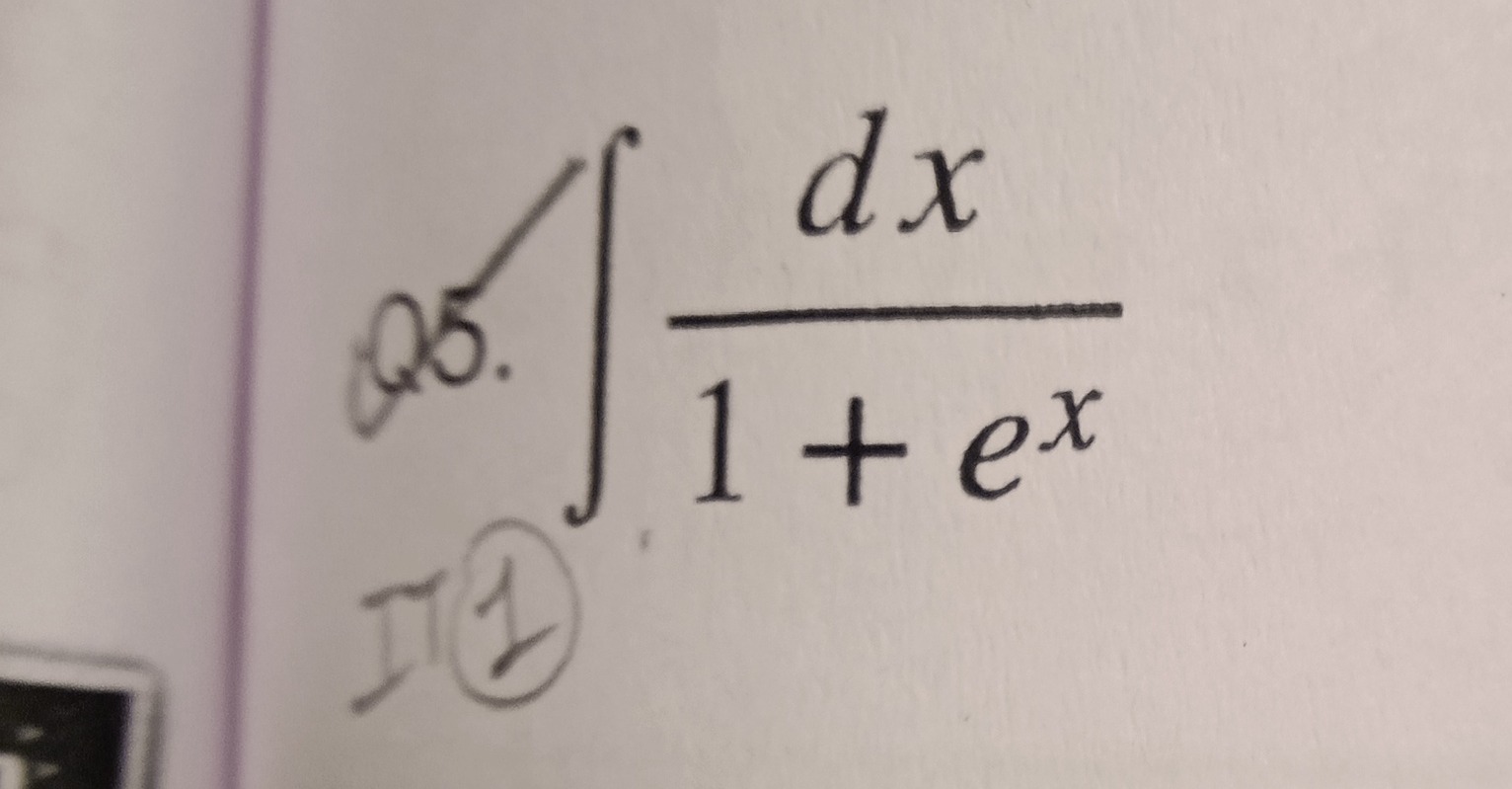
x−ln(1+ex)+C
Solution
To solve the integral ∫1+exdx, we can use a substitution method or algebraic manipulation.
Method 1: Algebraic Manipulation and Substitution
-
Multiply numerator and denominator by e−x: I=∫1+exdx=∫e−x(1+ex)e−xdx=∫e−x+1e−xdx
-
Perform a substitution: Let u=e−x+1. Differentiate u with respect to x: du=−e−xdx So, e−xdx=−du.
-
Substitute into the integral: I=∫u−du=−∫u1du
-
Integrate with respect to u: I=−ln∣u∣+C
-
Substitute back u=e−x+1: I=−ln∣e−x+1∣+C Since e−x>0 for all real x, e−x+1 is always positive, so we can remove the absolute value signs: I=−ln(e−x+1)+C
-
Simplify the expression: We can rewrite e−x+1 as ex1+1=ex1+ex. I=−ln(ex1+ex)+C Using logarithm properties, ln(ba)=lna−lnb: I=−(ln(1+ex)−ln(ex))+C I=−ln(1+ex)+ln(ex)+C Since ln(ex)=x: I=x−ln(1+ex)+C
Method 2: Substitution and Partial Fractions
-
Perform a substitution: Let t=ex. Differentiate t with respect to x: dt=exdx So, dx=exdt=tdt.
-
Substitute into the integral: I=∫1+t1⋅tdt=∫t(1+t)1dt
-
Decompose the integrand using partial fractions: We want to find A and B such that: t(1+t)1=tA+1+tB Multiply both sides by t(1+t): 1=A(1+t)+Bt Set t=0: 1=A(1+0)+B(0)⟹A=1. Set t=−1: 1=A(1−1)+B(−1)⟹1=−B⟹B=−1. So, the partial fraction decomposition is: t(1+t)1=t1−1+t1
-
Substitute back into the integral and integrate: I=∫(t1−1+t1)dt I=∫t1dt−∫1+t1dt I=ln∣t∣−ln∣1+t∣+C
-
Substitute back t=ex: I=ln∣ex∣−ln∣1+ex∣+C Since ex>0 and 1+ex>0, we can remove the absolute value signs: I=ln(ex)−ln(1+ex)+C Since ln(ex)=x: I=x−ln(1+ex)+C
Both methods yield the same result.
