Solveeit Logo
Login

Question

Question: If $x = b + c, y = c + a, z = a + b$, then find the value of $\frac{x^2 + y^2 + z^2 - xy - yz - zx}{...

If x=b+c,y=c+a,z=a+bx = b + c, y = c + a, z = a + b, then find the value of x2+y2+z2−xy−yz−zxa2+b2+c2−ab−bc−ca\frac{x^2 + y^2 + z^2 - xy - yz - zx}{a^2 + b^2 + c^2 - ab - bc - ca}

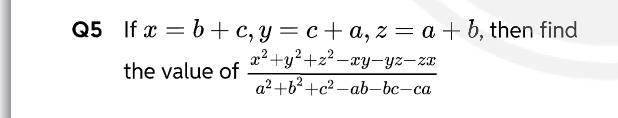
A

0

B

1

C

2

D

3

Answer

1

Explanation

Solution

Given the expression x2+y2+z2−xy−yz−zxa2+b2+c2−ab−bc−ca\frac{x^2 + y^2 + z^2 - xy - yz - zx}{a^2 + b^2 + c^2 - ab - bc - ca}, where x=b+cx = b + c, y=c+ay = c + a, and z=a+bz = a + b.

Let's substitute x=b+cx = b + c, y=c+ay = c + a, and z=a+bz = a + b into the numerator:

x2+y2+z2=(b+c)2+(c+a)2+(a+b)2=b2+2bc+c2+c2+2ca+a2+a2+2ab+b2=2(a2+b2+c2)+2(ab+bc+ca)x^2 + y^2 + z^2 = (b+c)^2 + (c+a)^2 + (a+b)^2 = b^2 + 2bc + c^2 + c^2 + 2ca + a^2 + a^2 + 2ab + b^2 = 2(a^2 + b^2 + c^2) + 2(ab + bc + ca)

xy+yz+zx=(b+c)(c+a)+(c+a)(a+b)+(a+b)(b+c)=bc+ab+c2+ca+ca+c2+a2+ab+ab+ac+b2+bc=a2+b2+c2+3(ab+bc+ca)xy + yz + zx = (b+c)(c+a) + (c+a)(a+b) + (a+b)(b+c) = bc + ab + c^2 + ca + ca + c^2 + a^2 + ab + ab + ac + b^2 + bc = a^2 + b^2 + c^2 + 3(ab + bc + ca)

Numerator =x2+y2+z2−(xy+yz+zx)=2(a2+b2+c2)+2(ab+bc+ca)−(a2+b2+c2+3(ab+bc+ca))=a2+b2+c2−(ab+bc+ca)= x^2 + y^2 + z^2 - (xy + yz + zx) = 2(a^2 + b^2 + c^2) + 2(ab + bc + ca) - (a^2 + b^2 + c^2 + 3(ab + bc + ca)) = a^2 + b^2 + c^2 - (ab + bc + ca)

Thus, the expression becomes:

a2+b2+c2−ab−bc−caa2+b2+c2−ab−bc−ca=1\frac{a^2 + b^2 + c^2 - ab - bc - ca}{a^2 + b^2 + c^2 - ab - bc - ca} = 1

Therefore, the value of the expression is 1.