Question
Question: If $\alpha$ & $\beta^2$ are the roots of the equation, $8x^2 - 10x + 3 =$ $\frac{1}{0}$, wehre $\bet...
If α & β2 are the roots of the equation, 8x2−10x+3= 01, wehre β2>21, then the equation whose roots are (α +iβ)100 & (α−iβ)100 is :
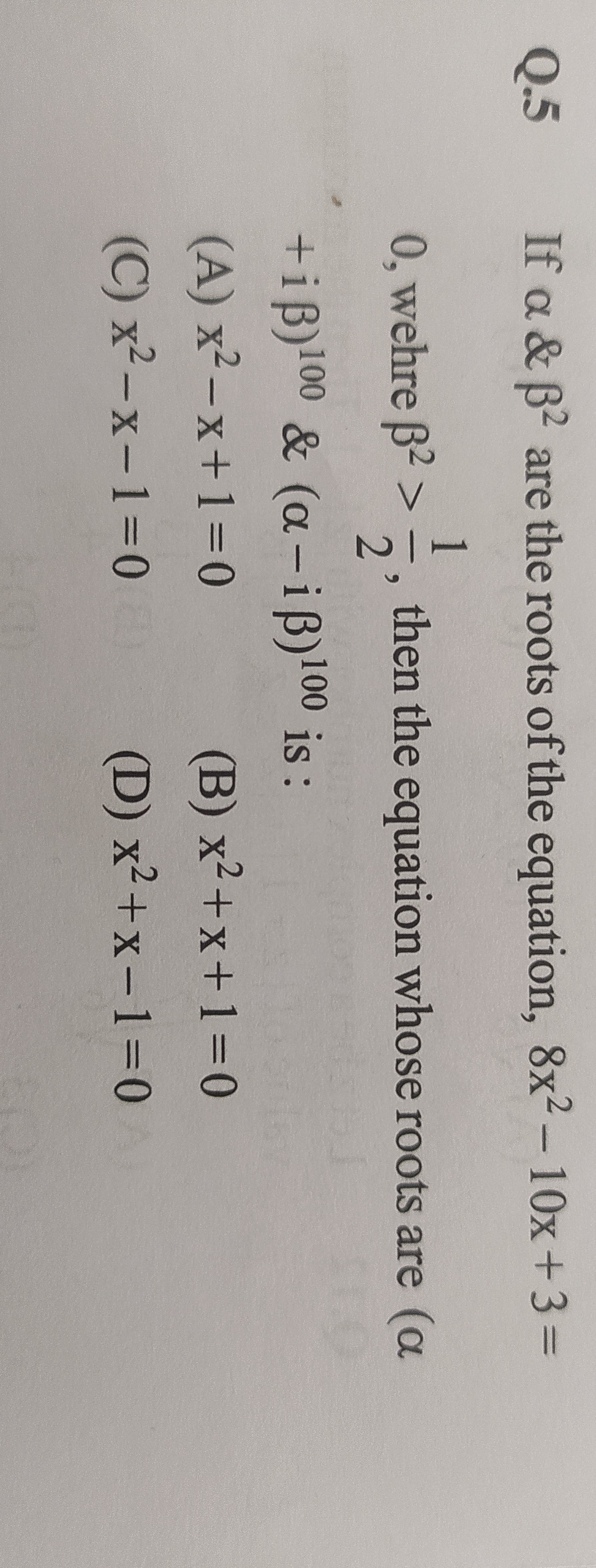
x2−x+1=0
x2+x+1=0
x2−x−1=0
x2+x−1=0
x^2+x+1=0
Solution
Solution:
-
The quadratic equation is 8x2−10x+3=0. Its discriminant D=102−4⋅8⋅3=100−96=4. Therefore, the roots are 1610±2=1612=43and168=21.
-
Given that one root is β2 and β2>21, we have β2=43 and so α=21. Then, β=23 (taking the positive value).
-
Now, α+iβ=21+i23=eiπ/3, α−iβ=21−i23=e−iπ/3.
-
Raising these to the 100th power: (α+iβ)100=ei(100π/3) (α−iβ)100=e−i(100π/3).
-
Reduce the exponent modulo 2π:
For positive exponent: 3100π−32π=3100π−96π=34π. Hence, one root is ei4π/3=−21−i23.
For negative exponent: −3100π+34π=3−100π+102π=32π. Hence, the other root is ei2π/3=−21+i23.
-
Their sum and product: Sum =ei4π/3+ei2π/3=(−21−i23)+(−21+i23)=−1. Product =ei(4π/3+2π/3)=ei2π=1.
-
The quadratic equation with roots r1 and r2 is: x2−(r1+r2)x+r1r2=x2−(−1)x+1=x2+x+1=0.
Explanation (minimal): Roots of 8x2−10x+3=0 are 43 and 21. Given β2>21, take β2=43 and α=21. Then, α±iβ=e±iπ/3 and raised to the 100th power yield ei4π/3 and ei2π/3. Their sum is −1 and product is 1, forming the quadratic x2+x+1=0.
