Question
Question: If $a(b-c)x^2+b(c-a)x+c(a-b)=0$ has equal roots, then P.T.o $\frac{1}{a}+\frac{1}{c}=\frac{2}{b}$...
If a(b−c)x2+b(c−a)x+c(a−b)=0 has equal roots, then P.T.o a1+c1=b2
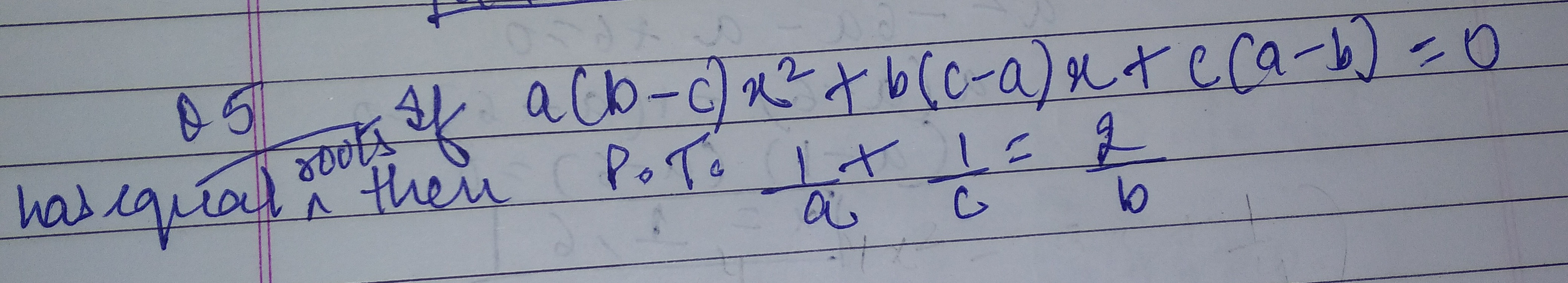
Answer
a1+c1=b2
Explanation
Solution
The sum of coefficients is a(b−c)+b(c−a)+c(a−b)=ab−ac+bc−ab+ac−bc=0. This implies x=1 is a root. For equal roots, x=1 must be a double root. For a quadratic Ax2+Bx+C=0 to have a double root at x=1, we need C=A. Thus, c(a−b)=a(b−c). Expanding gives ac−bc=ab−ac, so 2ac=ab+bc. Dividing by abc (assuming a,b,c=0) yields b2=c1+a1.
