Question

For what real values of k, the system of equations $x+2y+z=1; x+3y+4z=1; x+5y+10z=k^2$ has solution? Find the solution in each case.

Answer 1

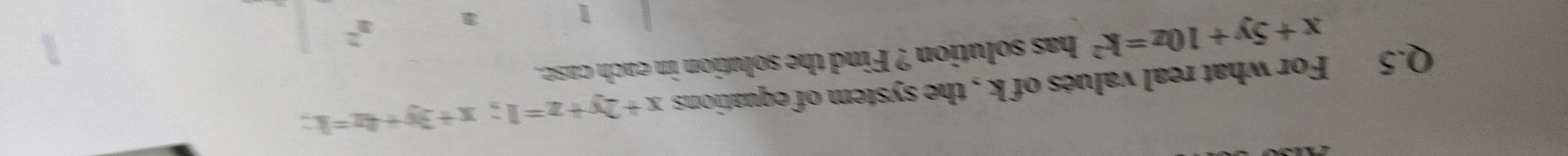
k = ± 1, solution is x=1+5t, y=-3t, z=t for t ∈ ℝ

Answer 2

The given system of linear equations is:

1. $x + 2y + z = 1$
2. $x + 3y + 4z = 1$
3. $x + 5y + 10z = k^2$

We can represent this system using an augmented matrix and apply elementary row operations to determine the conditions for a solution to exist and to find the solution.

The augmented matrix is: $M = \begin{pmatrix} 1 & 2 & 1 & | & 1 \\ 1 & 3 & 4 & | & 1 \\ 1 & 5 & 10 & | & k^2 \end{pmatrix}$

Perform row operations to transform the matrix into row echelon form:

Step 1: Make the elements below the first pivot (1) in the first column zero.

$R_2 \to R_2 - R_1$ $R_3 \to R_3 - R_1$

$M \sim \begin{pmatrix} 1 & 2 & 1 & | & 1 \\ 0 & 1 & 3 & | & 0 \\ 0 & 3 & 9 & | & k^2 - 1 \end{pmatrix}$

Step 2: Make the element below the second pivot (1) in the second column zero.

$R_3 \to R_3 - 3R_2$

$M \sim \begin{pmatrix} 1 & 2 & 1 & | & 1 \\ 0 & 1 & 3 & | & 0 \\ 0 & 0 & 0 & | & k^2 - 1 - 3(0) \end{pmatrix}$

$M \sim \begin{pmatrix} 1 & 2 & 1 & | & 1 \\ 0 & 1 & 3 & | & 0 \\ 0 & 0 & 0 & | & k^2 - 1 \end{pmatrix}$

For the system of equations to have a solution (i.e., be consistent), the last row of the augmented matrix must correspond to a true statement. The last row represents the equation $0x + 0y + 0z = k^2 - 1$.

For this equation to be true, we must have:

$k^2 - 1 = 0$ $k^2 = 1$ $k = \pm 1$

So, the system has a solution if and only if $k=1$ or $k=-1$.

Now, we find the solution in each case. Since the condition $k^2 - 1 = 0$ leads to the same reduced matrix, the solution will be the same for both $k=1$ and $k=-1$.

When $k = \pm 1$, the augmented matrix becomes:

$\begin{pmatrix} 1 & 2 & 1 & | & 1 \\ 0 & 1 & 3 & | & 0 \\ 0 & 0 & 0 & | & 0 \end{pmatrix}$

This matrix corresponds to the following system of equations:

1. $x + 2y + z = 1$
2. $y + 3z = 0$
3. $0 = 0$ (This indicates infinitely many solutions, as the rank of the coefficient matrix (2) is less than the number of variables (3)).

From equation (2), we can express $y$ in terms of $z$:

$y = -3z$

Substitute this into equation (1):

$x + 2(-3z) + z = 1$ $x - 6z + z = 1$ $x - 5z = 1$ $x = 1 + 5z$

Let $z = t$, where $t$ is any real number. Then, the solution is:

$z = t$ $y = -3t$ $x = 1 + 5t$

Thus, the solution set is $(x, y, z) = (1+5t, -3t, t)$ for any real number $t$.

The system has a solution for $k = \pm 1$. The solution in each case is $x = 1+5t$, $y = -3t$, $z = t$, where $t \in \mathbb{R}$.

In summary: The system of equations has a solution for real values of $k = \pm 1$. The solution in each case is given by $(x, y, z) = (1+5t, -3t, t)$, where $t$ is any real number.