Question
Question: Two conducting spheres of radii r1 and r2 are equally charged. The ratio of their potential is...
Two conducting spheres of radii r1 and r2 are equally charged. The ratio of their potential is
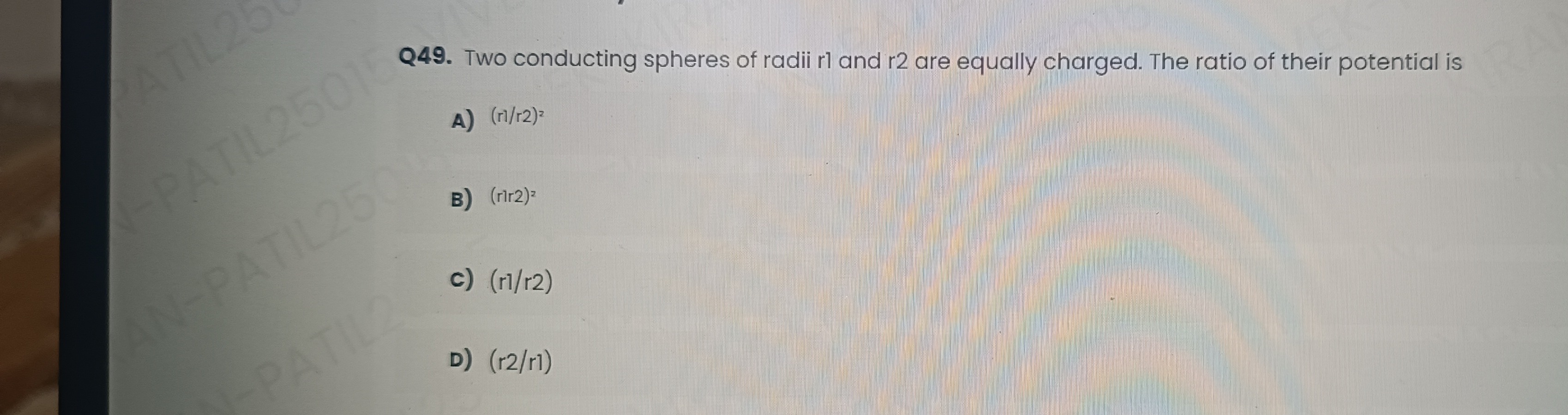
(r1/r2)²
(r1r2)²
(r1/r2)
(r2/r1)
(r2/r1)
Solution
Let the radii of the two conducting spheres be r1 and r2. The problem states that the spheres are "equally charged". Let the charge on each sphere be Q.
The electric potential (V) on the surface of a conducting sphere of radius r carrying a charge Q is given by the formula:
V=4πϵ01rQ
For the first sphere with radius r1 and charge Q, its potential V1 is:
V1=4πϵ01r1Q
For the second sphere with radius r2 and charge Q, its potential V2 is:
V2=4πϵ01r2Q
To find the ratio of their potentials, we divide V1 by V2:
V2V1=4πϵ01r2Q4πϵ01r1Q
The terms 4πϵ01 and Q are common in both the numerator and the denominator, so they cancel out:
V2V1=r21r11
V2V1=r11×r2
V2V1=r1r2
Thus, the ratio of their potentials is (r2/r1).
Explanation: The potential of a conducting sphere is directly proportional to its charge and inversely proportional to its radius. Since both spheres have the same charge, their potential ratio is simply the inverse ratio of their radii.
