Question

Number of ways in which two distinct natural numbers can be selected out of first 100 natural numbers so that sum of their cubes is multiple of 8 is N, then $\left[\frac{N}{200}\right]$ is equal to (where [.] denotes greatest integer function)

Answer 1

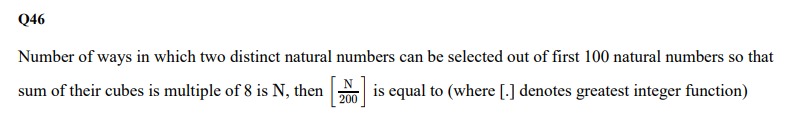
7

Answer 2

Let the two distinct natural numbers be $a$ and $b$, where $1 \le a < b \le 100$. We are given that the sum of their cubes, $a^3 + b^3$, is a multiple of 8. This can be written as $a^3 + b^3 \equiv 0 \pmod{8}$.

First, let's analyze the cube of a natural number modulo 8:

1. If $x$ is an even number: Let $x = 2k$ for some integer $k$. Then $x^3 = (2k)^3 = 8k^3$. So, $x^3 \equiv 0 \pmod{8}$ for any even number $x$.

2. If $x$ is an odd number: We can use the property that for any odd integer $x$, $x^3 \equiv x \pmod{8}$. This can be shown by factoring $x^3 - x = x(x^2 - 1) = x(x-1)(x+1)$. Since $x$ is odd, $x-1$ and $x+1$ are consecutive even integers. One of them must be a multiple of 4, and the other is a multiple of 2. Thus, their product $(x-1)(x+1)$ is a multiple of $2 \times 4 = 8$. Therefore, $x(x-1)(x+1)$ is a multiple of 8, which means $x^3 - x \equiv 0 \pmod{8}$, or $x^3 \equiv x \pmod{8}$. Let's verify this for possible odd residues modulo 8:

   • If $x \equiv 1 \pmod{8}$, $x^3 \equiv 1^3 \equiv 1 \pmod{8}$.
   • If $x \equiv 3 \pmod{8}$, $x^3 \equiv 3^3 = 27 \equiv 3 \pmod{8}$.
   • If $x \equiv 5 \pmod{8}$, $x^3 \equiv 5^3 = 125 \equiv 5 \pmod{8}$.
   • If $x \equiv 7 \pmod{8}$, $x^3 \equiv 7^3 = 343 \equiv 7 \pmod{8}$.

Now, let's consider the condition $a^3 + b^3 \equiv 0 \pmod{8}$ based on the parity of $a$ and $b$:

Case 1: Both $a$ and $b$ are even. If $a$ is even, $a^3 \equiv 0 \pmod{8}$. If $b$ is even, $b^3 \equiv 0 \pmod{8}$. Then $a^3 + b^3 \equiv 0 + 0 \equiv 0 \pmod{8}$. This condition is always satisfied if both $a$ and $b$ are even. There are 50 even numbers between 1 and 100 (2, 4, ..., 100). The number of ways to select two distinct even numbers is $\binom{50}{2}$. Number of ways = $\frac{50 \times 49}{2} = 25 \times 49 = 1225$.

Case 2: One number is even and the other is odd. Let $a$ be even and $b$ be odd. Then $a^3 \equiv 0 \pmod{8}$ and $b^3 \equiv b \pmod{8}$. So we need $a^3 + b^3 \equiv 0 + b \equiv b \pmod{8}$. For $a^3 + b^3 \equiv 0 \pmod{8}$, we would need $b \equiv 0 \pmod{8}$. However, $b$ is an odd number, so $b$ cannot be a multiple of 8. Therefore, $b \not\equiv 0 \pmod{8}$. Thus, this case is not possible.

Case 3: Both $a$ and $b$ are odd. If $a$ is odd, $a^3 \equiv a \pmod{8}$. If $b$ is odd, $b^3 \equiv b \pmod{8}$. So we need $a^3 + b^3 \equiv a + b \equiv 0 \pmod{8}$. This means that the sum of the two odd numbers $a$ and $b$ must be a multiple of 8. There are 50 odd numbers between 1 and 100 (1, 3, ..., 99). Let's classify these odd numbers based on their remainder modulo 8:

• $N_1$: Numbers $x \equiv 1 \pmod{8}$. These are $1, 9, \dots, 97$. Count: $1 + \lfloor \frac{97-1}{8} \rfloor = 1 + 12 = 13$ numbers.
• $N_3$: Numbers $x \equiv 3 \pmod{8}$. These are $3, 11, \dots, 99$. Count: $1 + \lfloor \frac{99-3}{8} \rfloor = 1 + 12 = 13$ numbers.
• $N_5$: Numbers $x \equiv 5 \pmod{8}$. These are $5, 13, \dots, 93$. Count: $1 + \lfloor \frac{93-5}{8} \rfloor = 1 + 11 = 12$ numbers.
• $N_7$: Numbers $x \equiv 7 \pmod{8}$. These are $7, 15, \dots, 95$. Count: $1 + \lfloor \frac{95-7}{8} \rfloor = 1 + 11 = 12$ numbers. Total odd numbers: $13+13+12+12 = 50$.

We need $a+b \equiv 0 \pmod{8}$. Let $a \pmod{8} = r_a$ and $b \pmod{8} = r_b$. Possible pairs $(r_a, r_b)$ such that $r_a+r_b \equiv 0 \pmod{8}$ and $r_a, r_b \in \{1, 3, 5, 7\}$:

1. $r_a = 1, r_b = 7$: $1+7 = 8 \equiv 0 \pmod{8}$. Number of ways to choose $a \in N_1$ and $b \in N_7$ is $13 \times 12 = 156$. Since $a \in N_1$ and $b \in N_7$, $a$ and $b$ are guaranteed to be distinct.
2. $r_a = 3, r_b = 5$: $3+5 = 8 \equiv 0 \pmod{8}$. Number of ways to choose $a \in N_3$ and $b \in N_5$ is $13 \times 12 = 156$. Since $a \in N_3$ and $b \in N_5$, $a$ and $b$ are guaranteed to be distinct. No other combinations of two distinct odd numbers will sum to a multiple of 8 (e.g., $1+1=2$, $3+3=6$, $5+5=10 \equiv 2$, $7+7=14 \equiv 6$).

Total number of ways for Case 3 = $156 + 156 = 312$.

Total number of ways $N$ is the sum of ways from Case 1 and Case 3. $N = 1225 + 312 = 1537$.

Finally, we need to calculate $\left[\frac{N}{200}\right]$. $\left[\frac{1537}{200}\right] = [7.685]$. The greatest integer less than or equal to 7.685 is 7.

The final answer is $\boxed{7}$.