Question
Question: If $x^3-px^2+qx-27=0$ has three positive roots where p, q>0 and $p+k+l^2=4l+10$ where $k, l \in \mat...
If x3−px2+qx−27=0 has three positive roots where p, q>0 and p+k+l2=4l+10 where k,l∈R, then the greatest value of k is
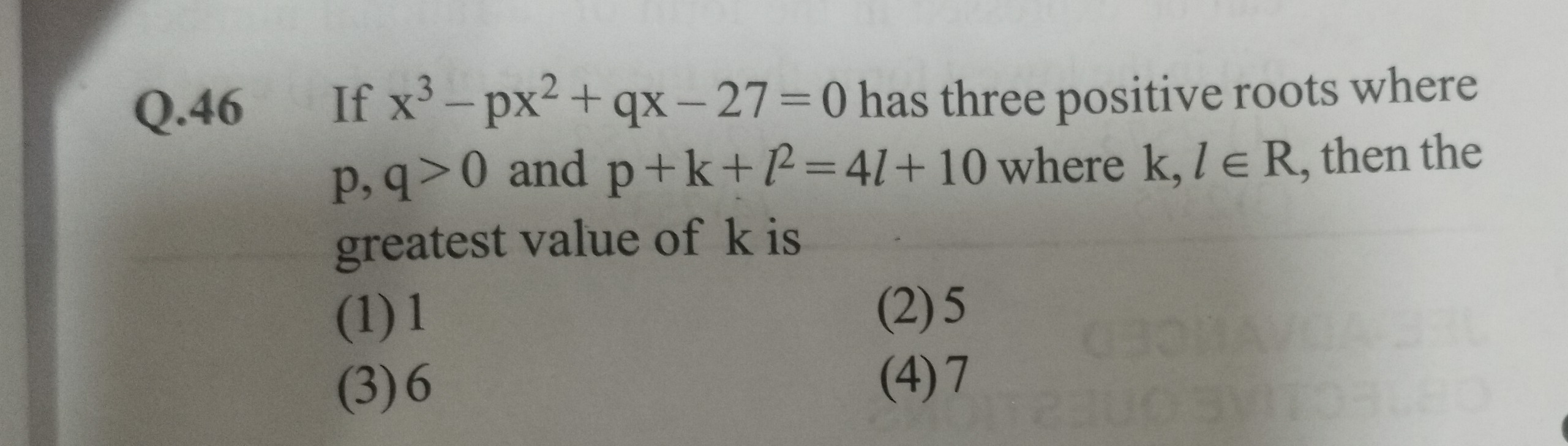
1
5
6
7
5
Solution
Let the three positive roots of the cubic equation x3−px2+qx−27=0 be α,β,γ. By Vieta's formulas:
- Sum of the roots: α+β+γ=p
- Product of the roots: αβγ=27
Since the roots are positive, we can apply the AM-GM inequality: 3α+β+γ≥3αβγ Substituting the values: 3p≥327 3p≥3 p≥9 The minimum value of p is 9.
We are given p+k+l2=4l+10. Rearranging for k: k=4l+10−l2−p k=10−p+(4l−l2) To maximize k, we need to maximize the term (4l−l2) and use the minimum value of p. The expression 4l−l2 can be maximized by completing the square: 4l−l2=−(l2−4l)=−((l−2)2−4)=4−(l−2)2 The maximum value of 4l−l2 is 4, which occurs when l=2.
Now, substitute the maximum value of 4l−l2 and the minimum value of p into the expression for k: kmax=10−pmin+(4l−l2)max kmax=10−9+4 kmax=5 The greatest value of k is 5.
