Question

What is the order of differential equation y" + 5y' + 6 = 0?

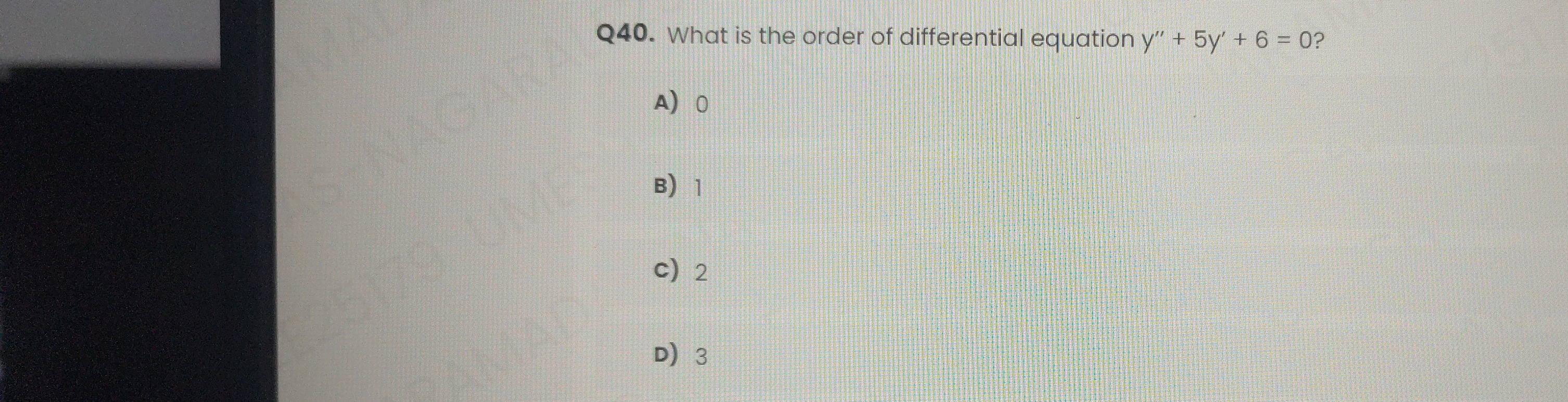
• A. 0
• B. 1
• C. 2
• D. 3

Answer 1

Answer: (C)

C

Answer 2

The order of a differential equation is defined as the order of the highest derivative appearing in the equation.

The given differential equation is:

$y'' + 5y' + 6 = 0$

Let's identify the derivatives present in the equation:

1. $y''$ represents the second derivative of y with respect to x ($\frac{d^2y}{dx^2}$). The order of this derivative is 2.

2. $y'$ represents the first derivative of y with respect to x ($\frac{dy}{dx}$). The order of this derivative is 1.

Comparing the orders of the derivatives, the highest order derivative present in the equation is $y''$, which is a second-order derivative.

Therefore, the order of the differential equation $y'' + 5y' + 6 = 0$ is 2.