Question
Question: Three short electric dipoles, each with dipole moment $P$, are placed at the vertices of an equilate...
Three short electric dipoles, each with dipole moment P, are placed at the vertices of an equilateral triangle of side length L. Each dipole's moment is oriented parallel to the opposite side of the triangle as shown in the figure. What is the magnitude of the electric field at the centroid of the triangle?
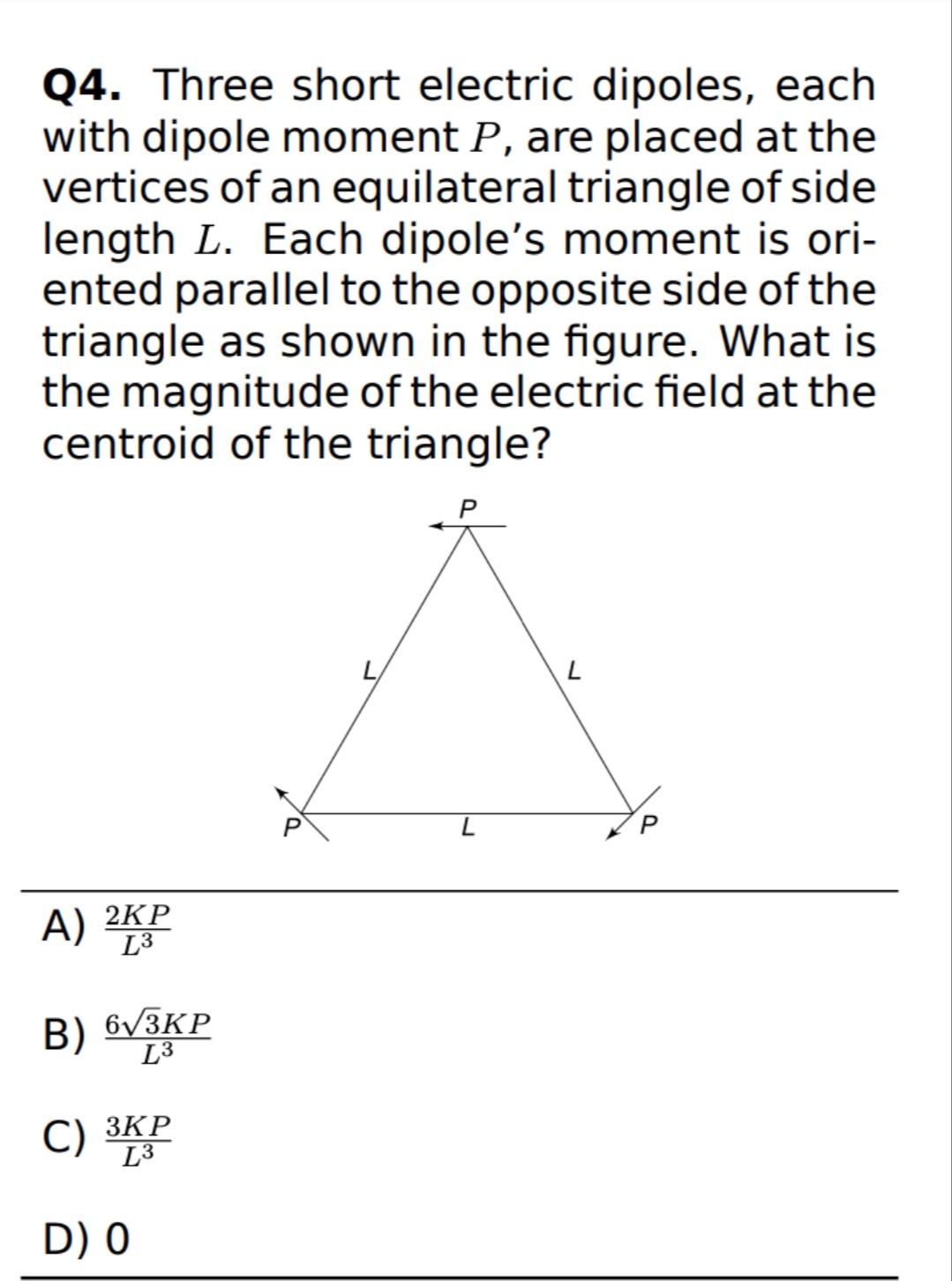
L32KP
L363KP
L33KP
0
L363KP
Solution
To find the magnitude of the electric field at the centroid of the equilateral triangle, we need to consider the contribution from each of the three dipoles.
-
Determine the distance from each vertex to the centroid.
Let the side length of the equilateral triangle be L.
The height of the triangle is h=Lsin(60∘)=L23.
The centroid is located at a distance r from each vertex, where r=32h.
So, r=32(L23)=3L.
-
Determine the orientation of each dipole relative to the line connecting it to the centroid.
In an equilateral triangle, the line segment from a vertex to the centroid is also the median to the opposite side. The median is perpendicular to the opposite side if the triangle is isosceles (and thus equilateral).
Since each dipole moment is oriented parallel to the opposite side, the line connecting the dipole to the centroid (which is the median) is perpendicular to the dipole moment vector.
This means the centroid lies on the equatorial line of each dipole.
-
Calculate the magnitude of the electric field due to a single dipole at the centroid.
For a short electric dipole, the electric field on its equatorial line (perpendicular bisector) at a distance r from the center of the dipole is given by:
E=r3KP
Substituting r=3L:
Esingle=(L/3)3KP=L3/(33)KP=L333KP.
The direction of the electric field on the equatorial line is antiparallel to the dipole moment vector.
-
Vector sum of the electric fields.
Let's set up a coordinate system with the centroid at the origin (0,0).
Let the vertices be A (top), B (bottom-left), and C (bottom-right).
-
Dipole at A (top vertex):
The dipole moment PA is parallel to the base BC. From the figure, it points to the left.
So, PA=−Pi^.
The electric field EA at the centroid is antiparallel to PA.
EA=Esinglei^=L333KPi^.
-
Dipole at B (bottom-left vertex):
The dipole moment PB is parallel to the side AC. The side AC makes an angle of 60∘ with the horizontal. From the figure, PB points towards top-left. This means its direction is 120∘ from the positive x-axis.
PB=P(cos(120∘)i^+sin(120∘)j^)=P(−21i^+23j^).
The electric field EB at the centroid is antiparallel to PB.
EB=−Esingle(cos(120∘)i^+sin(120∘)j^)=Esingle(21i^−23j^).
-
Dipole at C (bottom-right vertex):
The dipole moment PC is parallel to the side AB. The side AB makes an angle of 120∘ with the horizontal. From the figure, PC points towards top-right. This means its direction is 60∘ from the positive x-axis.
PC=P(cos(60∘)i^+sin(60∘)j^)=P(21i^+23j^).
The electric field EC at the centroid is antiparallel to PC.
EC=−Esingle(cos(60∘)i^+sin(60∘)j^)=Esingle(−21i^−23j^).
-
-
Calculate the net electric field.
Enet=EA+EB+EC
Enet=Esinglei^+Esingle(21i^−23j^)+Esingle(−21i^−23j^)
Combine the components:
Enet=Esingle[(1+21−21)i^+(0−23−23)j^]
Enet=Esingle[i^−3j^]
-
Calculate the magnitude of the net electric field.
∣Enet∣=Esingle(1)2+(−3)2=Esingle1+3=Esingle4=2Esingle
Substitute the value of Esingle:
∣Enet∣=2×L333KP=L363KP.
The final answer is L363KP.
