Question

\lim_{x\to 0^+} \left(\frac{(1+x)^{\frac{1}{x}}}{e}\right)^{\frac{1}{x}} =

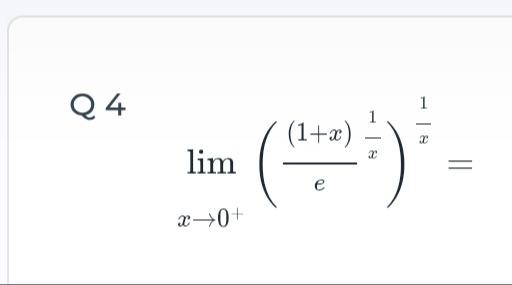
Answer 1

e^{-1/2}

Answer 2

Let the limit be $L$. $L = \lim_{x\to 0^+} \left(\frac{(1+x)^{\frac{1}{x}}}{e}\right)^{\frac{1}{x}}$ We can rewrite the expression as: $L = \lim_{x\to 0^+} \exp\left( \frac{1}{x} \ln\left(\frac{(1+x)^{\frac{1}{x}}}{e}\right) \right)$ $L = \lim_{x\to 0^+} \exp\left( \frac{1}{x} \left( \frac{1}{x}\ln(1+x) - \ln(e) \right) \right)$ $L = \lim_{x\to 0^+} \exp\left( \frac{\ln(1+x) - x}{x^2} \right)$ Now we evaluate the limit of the exponent using L'Hopital's Rule: $\lim_{x\to 0^+} \frac{\ln(1+x) - x}{x^2}$ This is of the form $\frac{0}{0}$. Applying L'Hopital's Rule: $\lim_{x\to 0^+} \frac{\frac{1}{1+x} - 1}{2x} = \lim_{x\to 0^+} \frac{\frac{1 - (1+x)}{1+x}}{2x} = \lim_{x\to 0^+} \frac{-x}{2x(1+x)}$ $= \lim_{x\to 0^+} \frac{-1}{2(1+x)} = -\frac{1}{2}$ Therefore, $L = e^{-1/2}$.