Question
Question: Let f: R$^+$ $\rightarrow$ R defined as f(x) = e$^x$ + lnx and g = f$^{-1}$ then correct statement(s...
Let f: R+ → R defined as f(x) = ex + lnx and g = f−1 then correct statement(s) is/are-
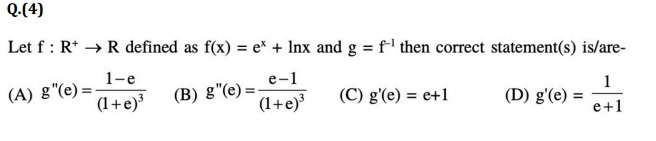
g''(e) = (1+e)31−e
g''(e) = (1+e)3e−1
g'(e) = e+1
g'(e) = e+11
The correct statements are (A) and (D).
Solution
Let the given function be f(x)=ex+lnx defined for x∈R+=(0,∞). The inverse function is g=f−1. We need to evaluate g′(e) and g′′(e).
First, find the value of x such that f(x)=e. ex+lnx=e. By inspection, for x=1, we have e1+ln1=e+0=e. So, f(1)=e. This means g(e)=1.
Next, find the first derivative of f(x): f′(x)=dxd(ex+lnx)=ex+x1. Evaluate f′(x) at x=1: f′(1)=e1+11=e+1.
The formula for the derivative of an inverse function g(y)=f−1(y) is g′(y)=f′(x)1, where y=f(x). We want to find g′(e). Here y=e, which corresponds to x=1. g′(e)=f′(1)1=e+11.
Now, find the second derivative of f(x): f′′(x)=dxd(ex+x−1)=ex−x−2=ex−x21. Evaluate f′′(x) at x=1: f′′(1)=e1−121=e−1.
The formula for the second derivative of an inverse function is g′′(y)=−(f′(x))3f′′(x), where y=f(x). We want to find g′′(e). Here y=e, which corresponds to x=1. g′′(e)=−(f′(1))3f′′(1)=−(e+1)3e−1=(e+1)3−(e−1)=(e+1)31−e.
Comparing our results with the given options: (A) g′′(e)=(1+e)31−e. This matches our result. (B) g′′(e)=(1+e)3e−1. This does not match our result. (C) g′(e)=e+1. This does not match our result. (D) g′(e)=e+11. This matches our result.
Therefore, the correct statements are (A) and (D).
Explanation:
- Find x such that f(x)=e. ex+lnx=e⟹x=1. Thus g(e)=1.
- Calculate f′(x)=ex+1/x and f′′(x)=ex−1/x2.
- Evaluate f′(1)=e+1 and f′′(1)=e−1.
- Use the formula g′(y)=1/f′(x) at y=e,x=1. g′(e)=1/f′(1)=1/(e+1).
- Use the formula g′′(y)=−f′′(x)/(f′(x))3 at y=e,x=1. g′′(e)=−f′′(1)/(f′(1))3=−(e−1)/(e+1)3=(1−e)/(e+1)3.
- Match the results with the given options.
