Question

$\int \sqrt{\frac{x}{1-x^3}}dx$

Answer 1

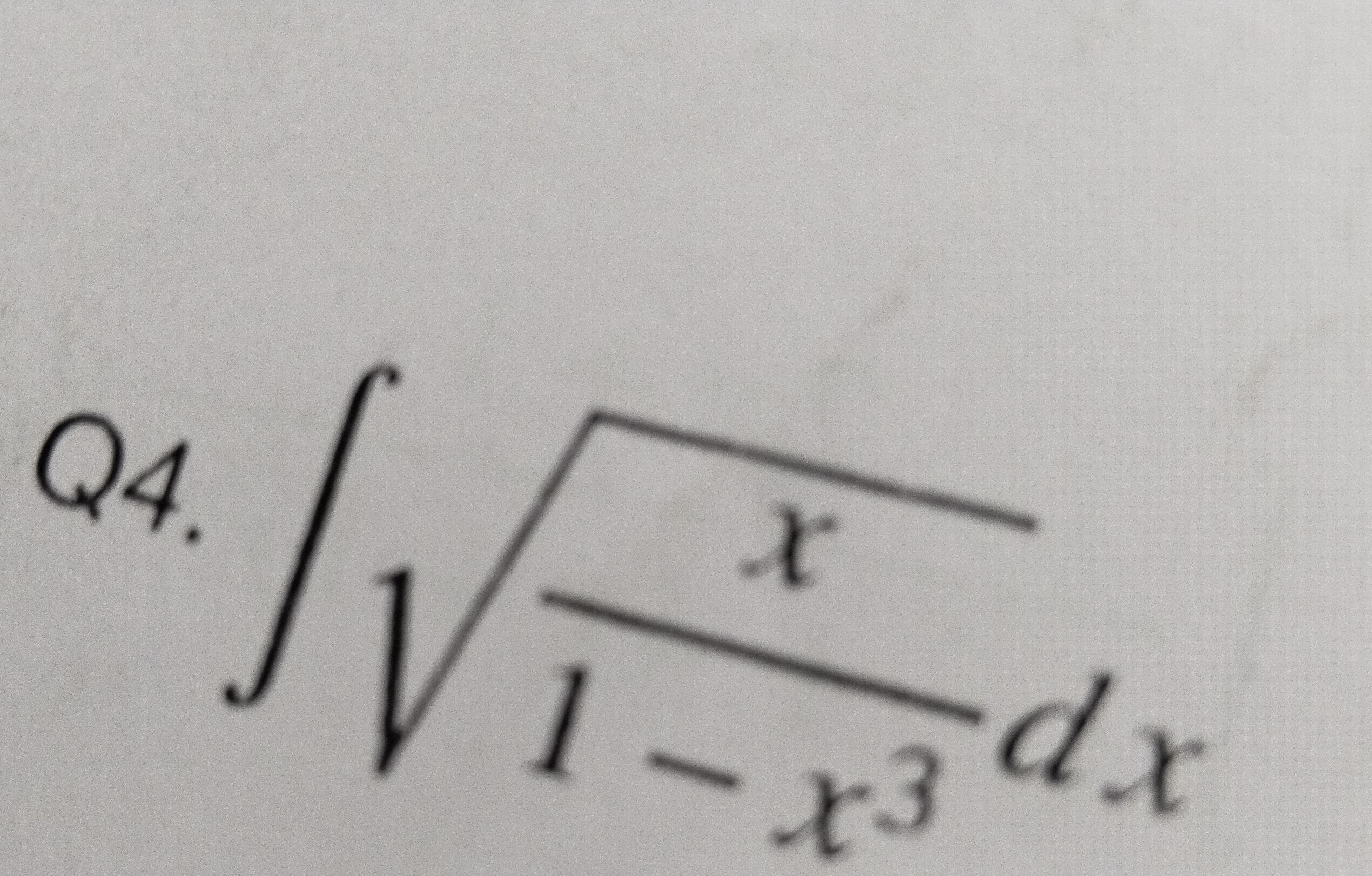
$\frac{2}{3} \arcsin(x^{3/2}) + C$

Answer 2

The problem asks to evaluate the indefinite integral $\int \sqrt{\frac{x}{1-x^3}}dx$.

Explanation of the solution:

1. Rewrite the integrand: The integrand is $\sqrt{\frac{x}{1-x^3}}$. This can be written as $\frac{\sqrt{x}}{\sqrt{1-x^3}}$. Notice that the term $x^3$ in the denominator can be expressed as $(x^{3/2})^2$. So, the integral becomes $\int \frac{\sqrt{x}}{\sqrt{1-(x^{3/2})^2}} dx$.

2. Choose a substitution: The form $\frac{f'(x)}{\sqrt{1-(f(x))^2}}$ suggests using the substitution $u = f(x)$, which leads to an integral of the form $\int \frac{1}{\sqrt{1-u^2}}du = \arcsin u + C$. Let $u = x^{3/2}$.

3. Calculate $du$: Differentiate $u$ with respect to $x$: $du = \frac{d}{dx}(x^{3/2}) dx$ $du = \frac{3}{2} x^{3/2 - 1} dx$ $du = \frac{3}{2} x^{1/2} dx$ $du = \frac{3}{2} \sqrt{x} dx$

4. Express $\sqrt{x} dx$ in terms of $du$: From the expression for $du$, we can write: $\sqrt{x} dx = \frac{2}{3} du$.

5. Substitute into the integral: Substitute $u = x^{3/2}$ and $\sqrt{x} dx = \frac{2}{3} du$ into the integral: $\int \frac{1}{\sqrt{1-(x^{3/2})^2}} \cdot \sqrt{x} dx = \int \frac{1}{\sqrt{1-u^2}} \cdot \frac{2}{3} du$

6. Evaluate the integral: Take the constant $\frac{2}{3}$ outside the integral: $= \frac{2}{3} \int \frac{1}{\sqrt{1-u^2}} du$ Recall the standard integral formula: $\int \frac{1}{\sqrt{1-y^2}} dy = \arcsin y + C$. Applying this formula, we get: $= \frac{2}{3} \arcsin u + C$

7. Substitute back to the original variable: Replace $u$ with $x^{3/2}$: $= \frac{2}{3} \arcsin(x^{3/2}) + C$

The domain of the integrand requires $x \ge 0$ and $1-x^3 > 0$, which means $0 \le x < 1$. This ensures that $x^{3/2}$ is in the range $[0, 1)$, for which $\arcsin(x^{3/2})$ is well-defined.