Question

$\int \sqrt{\frac{x}{1-x^3}}dx$

Answer 1

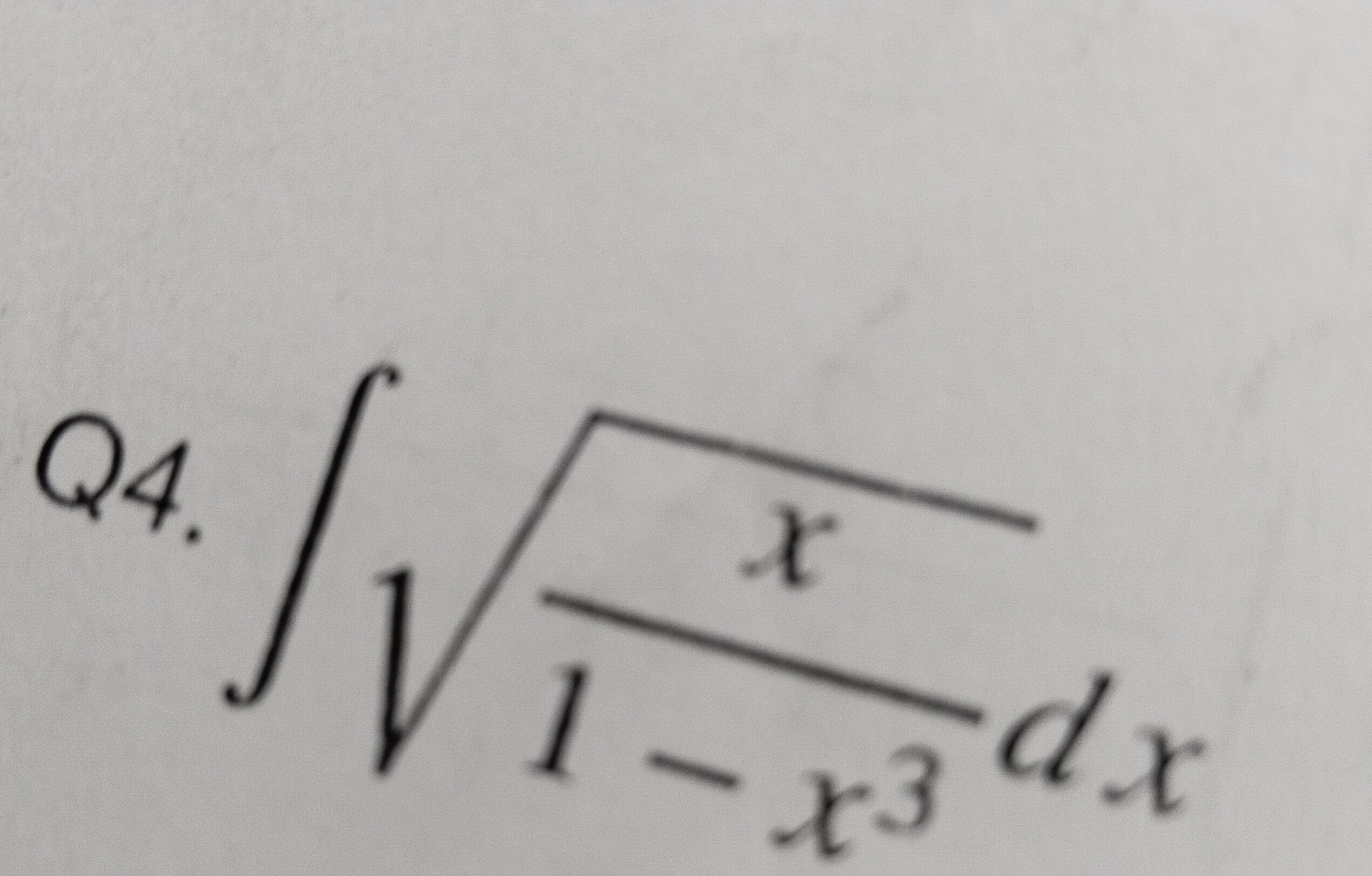
$\frac{2}{3} \arcsin(x^{3/2}) + C$

Answer 2

To evaluate the integral $\int \sqrt{\frac{x}{1-x^3}}dx$, we can use the method of substitution.

Step 1: Rewrite the integrand

The given integral can be written as:

$$\int \frac{\sqrt{x}}{\sqrt{1-x^3}}dx$$

Notice that $x^3$ can be expressed as $(x^{3/2})^2$. This form, $\sqrt{1-u^2}$ in the denominator, is characteristic of the derivative of $\arcsin(u)$.

Step 2: Choose an appropriate substitution

Let $u = x^{3/2}$.

Step 3: Find the differential $du$

Differentiate $u$ with respect to $x$:

$$\frac{du}{dx} = \frac{d}{dx}(x^{3/2}) = \frac{3}{2}x^{(3/2)-1} = \frac{3}{2}x^{1/2} = \frac{3}{2}\sqrt{x}$$

From this, we can express $\sqrt{x}dx$ in terms of $du$:

$$du = \frac{3}{2}\sqrt{x}dx \implies \sqrt{x}dx = \frac{2}{3}du$$

Step 4: Substitute into the integral

Now substitute $u$ and $dx$ into the integral:

$$\int \frac{1}{\sqrt{1-(x^{3/2})^2}} (\sqrt{x}dx) = \int \frac{1}{\sqrt{1-u^2}} \left(\frac{2}{3}du\right)$$ $$= \frac{2}{3} \int \frac{1}{\sqrt{1-u^2}}du$$

Step 5: Evaluate the standard integral

The integral $\int \frac{1}{\sqrt{1-u^2}}du$ is a standard integral, which evaluates to $\arcsin(u) + C$.

$$= \frac{2}{3} \arcsin(u) + C$$

Step 6: Substitute back to the original variable

Finally, substitute $u = x^{3/2}$ back into the result:

$$= \frac{2}{3} \arcsin(x^{3/2}) + C$$

The domain of the integrand requires $x \ge 0$ and $1-x^3 > 0$, so $0 \le x < 1$. In this domain, $x^{3/2}$ is well-defined and lies in $[0, 1)$, which is within the domain of $\arcsin$.