Question

If $2x + 3y + 4z = 0$, then prove that:

$8x^3 + 27y^3 + 64z^3 = 72xyz$

Answer 1

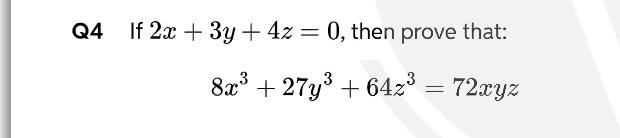
Given $2x + 3y + 4z = 0$, we can prove that $8x^3 + 27y^3 + 64z^3 = 72xyz$ using the identity: if $a+b+c=0$, then $a^3+b^3+c^3 = 3abc$. Let $a = 2x$, $b = 3y$, $c = 4z$. Then the condition becomes $a+b+c = 0$. Substituting $a=2x, b=3y, c=4z$ into the identity, we get $(2x)^3 + (3y)^3 + (4z)^3 = 3(2x)(3y)(4z)$, which simplifies to $8x^3 + 27y^3 + 64z^3 = 72xyz$.

Answer 2

Given the condition $2x + 3y + 4z = 0$, we aim to prove that $8x^3 + 27y^3 + 64z^3 = 72xyz$.

Let $a = 2x$, $b = 3y$, and $c = 4z$. Then the given condition $2x + 3y + 4z = 0$ can be rewritten as:

$a + b + c = 0$

We will use the algebraic identity that states if the sum of three terms is zero, then the sum of their cubes is equal to three times their product:

If $a + b + c = 0$, then $a^3 + b^3 + c^3 = 3abc$.

Since $a + b + c = 0$, we can apply this identity:

$a^3 + b^3 + c^3 = 3abc$

Now, substitute back the expressions for $a, b, c$ in terms of $x, y, z$:

$(2x)^3 + (3y)^3 + (4z)^3 = 3(2x)(3y)(4z)$

Calculate the cubes and the product:

$(2x)^3 = 8x^3$

$(3y)^3 = 27y^3$

$(4z)^3 = 64z^3$

$3(2x)(3y)(4z) = 72xyz$

Substituting these back into the identity $a^3 + b^3 + c^3 = 3abc$:

$8x^3 + 27y^3 + 64z^3 = 72xyz$

Thus, the identity is proven.