Question

If P = $\begin{bmatrix} 1 & k & 3 \\ 1 & 3 & 3 \\ 2 & 4 & 4 \end{bmatrix}$ is the adjoint of a 3 × 3 matrix Q and det.(Q) = 6, then k is equal to

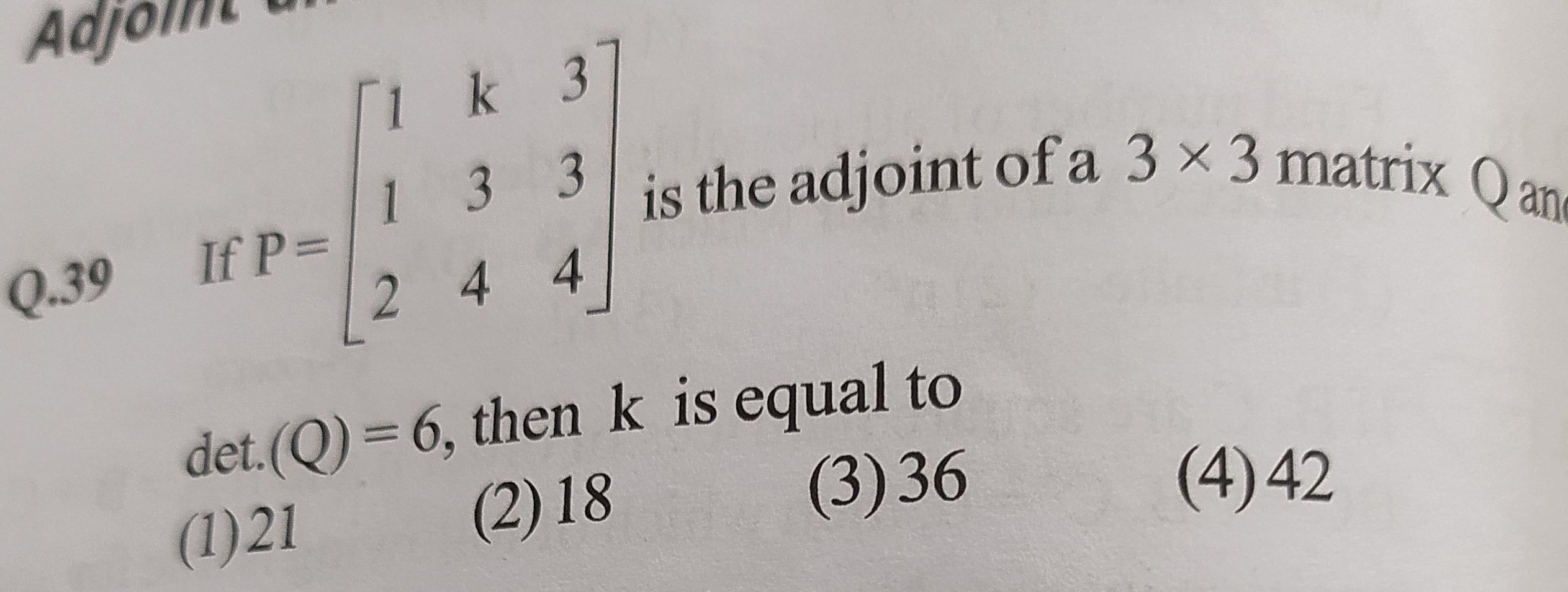
• A. 21
• B. 18
• C. 36
• D. 42

Answer 1

Answer: (A)

21

Answer 2

Let P be the given matrix and Q be a 3 × 3 matrix such that P = adj(Q). We are given that det(Q) = 6.

For an $n \times n$ matrix Q, the determinant of its adjoint is given by the property:

$\det(\text{adj}(Q)) = (\det(Q))^{n-1}$

In this case, Q is a 3 × 3 matrix, so n = 3. Given P = adj(Q), we have $\det(P) = \det(\text{adj}(Q))$. Using the property, $\det(P) = (\det(Q))^{3-1} = (\det(Q))^2$. Given $\det(Q) = 6$, we have $\det(P) = 6^2 = 36$.

Now, we calculate the determinant of the matrix P in terms of k: $P = \begin{bmatrix} 1 & k & 3 \\ 1 & 3 & 3 \\ 2 & 4 & 4 \end{bmatrix}$

$\det(P) = 1 \begin{vmatrix} 3 & 3 \\ 4 & 4 \end{vmatrix} - k \begin{vmatrix} 1 & 3 \\ 2 & 4 \end{vmatrix} + 3 \begin{vmatrix} 1 & 3 \\ 2 & 4 \end{vmatrix}$

$\det(P) = 1((3 \times 4) - (3 \times 4)) - k((1 \times 4) - (3 \times 2)) + 3((1 \times 4) - (3 \times 2))$

$\det(P) = 1(12 - 12) - k(4 - 6) + 3(4 - 6)$

$\det(P) = 1(0) - k(-2) + 3(-2)$

$\det(P) = 0 + 2k - 6$

$\det(P) = 2k - 6$

We have two expressions for $\det(P)$: $\det(P) = 36$ and $\det(P) = 2k - 6$.

Equating these two expressions:

$2k - 6 = 36$

$2k = 36 + 6$

$2k = 42$

$k = \frac{42}{2}$

$k = 21$

Thus, the value of k is 21.