Question

find value(s) of 'm' for which Q.E $3x^2+4mx+2=0$ and $2x^2+5x-2=0$ have a common root.

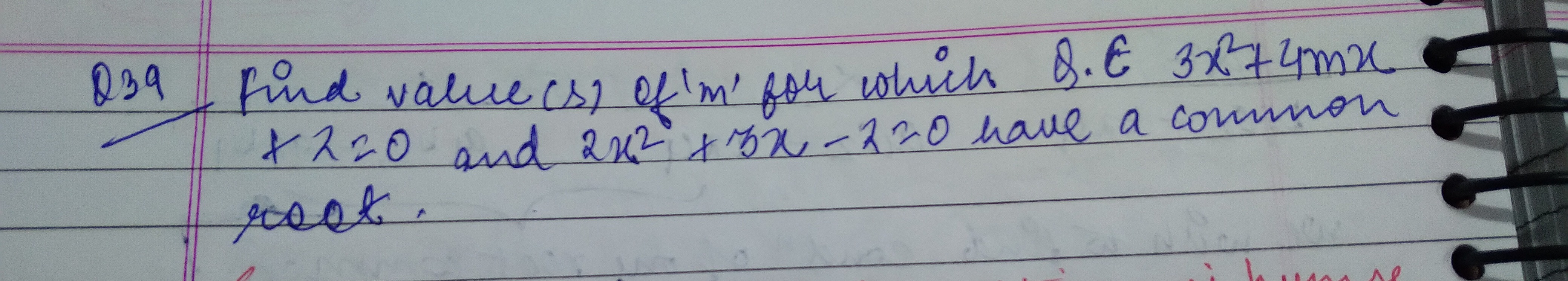
Answer 1

The values of m are $\frac{5(1 + \sqrt{41})}{16}, \frac{5(1 - \sqrt{41})}{16}$.

Answer 2

Let the common root be $\alpha$. The two equations are $3\alpha^2 + 4m\alpha + 2 = 0$ and $2\alpha^2 + 5\alpha - 2 = 0$. Using the condition $(c_1a_2 - c_2a_1)^2 = (a_1b_2 - a_2b_1)(b_1c_2 - b_2c_1)$, with $a_1=3, b_1=4m, c_1=2$ and $a_2=2, b_2=5, c_2=-2$, we get $(10)^2 = (15-8m)(-8m-10)$. This simplifies to $100 = 64m^2 - 40m - 150$, leading to the quadratic equation $32m^2 - 20m - 125 = 0$. Solving this equation for $m$ yields $m = \frac{5(1 \pm \sqrt{41})}{16}$.