Question

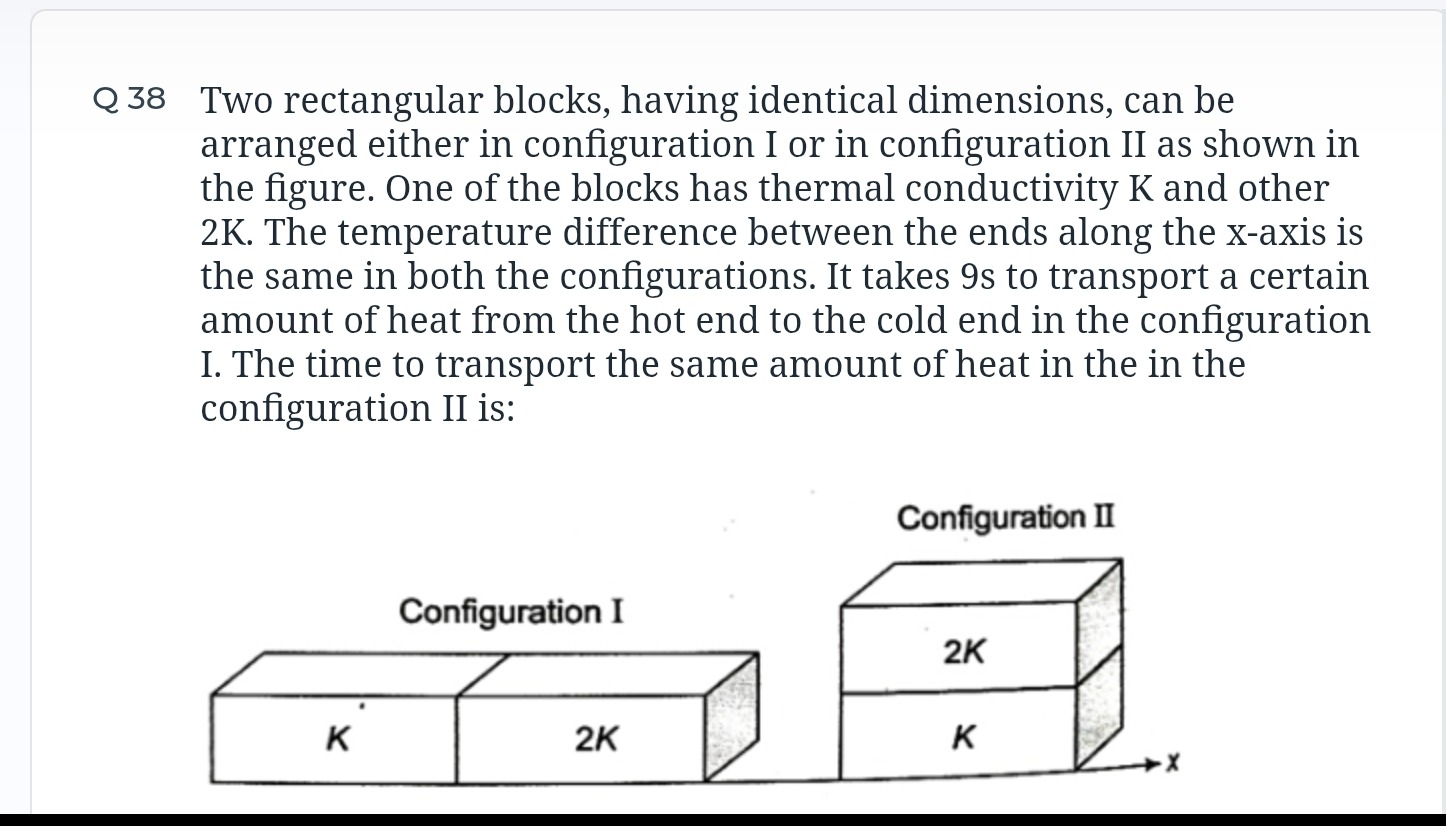
Two rectangular blocks, having identical dimensions, can be arranged either in configuration I or in configuration II as shown in the figure. One of the blocks has thermal conductivity K and other 2K. The temperature difference between the ends along the x-axis is the same in both the configurations. It takes 9s to transport a certain amount of heat from the hot end to the cold end in the configuration I. The time to transport the same amount of heat in the in the configuration II is:

• A. 2 s
• B. 3 s
• C. 4 s
• D. 6 s

Answer 1

Answer: (A)

2 s

Answer 2

The rate of heat transfer is given by $dQ/dt = kA(\Delta T/L)$, and the thermal resistance is $R = L/(kA)$. The time taken is $t = Q \cdot R / \Delta T$. Since $Q$ and $\Delta T$ are constant, time is proportional to thermal resistance.

Let the dimensions of each block be $l \times w \times h$.

Configuration I (series): The total length is $2l$, and the area is $wh$. $R_I = \frac{l}{K(wh)} + \frac{l}{2K(wh)} = \frac{3l}{2Kwh}$. $t_I \propto R_I$.

Configuration II (parallel): The length is $l$, and the effective area is $2wh$. $\frac{1}{R_{II}} = \frac{1}{l/(Kwh)} + \frac{1}{l/(2Kwh)} = \frac{Kwh}{l} + \frac{2Kwh}{l} = \frac{3Kwh}{l}$. $R_{II} = \frac{l}{3Kwh}$. $t_{II} \propto R_{II}$.

Comparing resistances: $\frac{t_{II}}{t_I} = \frac{R_{II}}{R_I} = \frac{l/(3Kwh)}{3l/(2Kwh)} = \frac{1}{3} \times \frac{2}{3} = \frac{2}{9}$. Given $t_I = 9s$, then $t_{II} = \frac{2}{9} \times 9s = 2s$.