Solveeit Logo
Login

Question

Question: Prove that $(\csc \theta + \sin \theta)(\csc \theta - \sin \theta) = \cot^2 \theta + \cos^2 \theta$...

Prove that (csc⁡θ+sin⁡θ)(csc⁡θ−sin⁡θ)=cot⁡2θ+cos⁡2θ(\csc \theta + \sin \theta)(\csc \theta - \sin \theta) = \cot^2 \theta + \cos^2 \theta

Answer

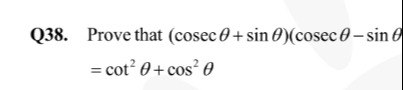
The identity (csc⁡θ+sin⁡θ)(csc⁡θ−sin⁡θ)=cot⁡2θ+cos⁡2θ(\csc \theta + \sin \theta)(\csc \theta - \sin \theta) = \cot^2 \theta + \cos^2 \theta is proven.

Explanation

Solution

To prove the identity (csc⁡θ+sin⁡θ)(csc⁡θ−sin⁡θ)=cot⁡2θ+cos⁡2θ(\csc \theta + \sin \theta)(\csc \theta - \sin \theta) = \cot^2 \theta + \cos^2 \theta, we start with the Left Hand Side (LHS) and manipulate it using fundamental trigonometric identities.

  1. Apply the difference of squares formula: The LHS is in the form (a+b)(a−b)(a+b)(a-b), where a=csc⁡θa = \csc \theta and b=sin⁡θb = \sin \theta. Using the formula (a+b)(a−b)=a2−b2(a+b)(a-b) = a^2 - b^2: LHS=(csc⁡θ+sin⁡θ)(csc⁡θ−sin⁡θ)=csc⁡2θ−sin⁡2θ\text{LHS} = (\csc \theta + \sin \theta)(\csc \theta - \sin \theta) = \csc^2 \theta - \sin^2 \theta

  2. Use Pythagorean Identities: We use the Pythagorean identities:

    • csc⁡2θ=1+cot⁡2θ\csc^2 \theta = 1 + \cot^2 \theta
    • sin⁡2θ=1−cos⁡2θ\sin^2 \theta = 1 - \cos^2 \theta

    Substitute these into the expression for LHS: LHS=(1+cot⁡2θ)−(1−cos⁡2θ)\text{LHS} = (1 + \cot^2 \theta) - (1 - \cos^2 \theta)

  3. Simplify the expression: Remove the parentheses and combine like terms: LHS=1+cot⁡2θ−1+cos⁡2θ\text{LHS} = 1 + \cot^2 \theta - 1 + \cos^2 \theta LHS=cot⁡2θ+cos⁡2θ\text{LHS} = \cot^2 \theta + \cos^2 \theta

This result is identical to the Right Hand Side (RHS). Therefore, the identity is proven.