Solveeit Logo
Login

Question

Question: Prove $\frac{sin \theta}{(1+cos \theta)} + \frac{(1+cos \theta)}{sin \theta} = 2 cosec \theta$...

Prove sinθ(1+cosθ)+(1+cosθ)sinθ=2cosecθ\frac{sin \theta}{(1+cos \theta)} + \frac{(1+cos \theta)}{sin \theta} = 2 cosec \theta

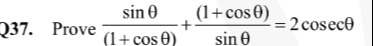
Answer

The identity sin⁡θ(1+cos⁡θ)+(1+cos⁡θ)sin⁡θ=2csc⁡θ\frac{\sin \theta}{(1+\cos \theta)} + \frac{(1+\cos \theta)}{\sin \theta} = 2 \csc \theta is proven to be true.

Explanation

Solution

Combine fractions on LHS. Simplify numerator using sin⁡2θ+cos⁡2θ=1\sin^2\theta + \cos^2\theta = 1 to get 2(1+cos⁡θ)2(1+\cos\theta). Cancel (1+cos⁡θ)(1+\cos\theta) from numerator and denominator. Result is 2/sin⁡θ2/\sin\theta, which equals 2csc⁡θ2\csc\theta (RHS).