Question
Question: If $A = \begin{bmatrix} 2\sin^2 \theta & 0 \\ \sin^2 \theta & \sin^2 \theta \end{bmatrix}$ and $A^{-...
If A=[2sin2θsin2θ0sin2θ] and A−1=[1−102] then the number of possible values of θ in [−π,π], is
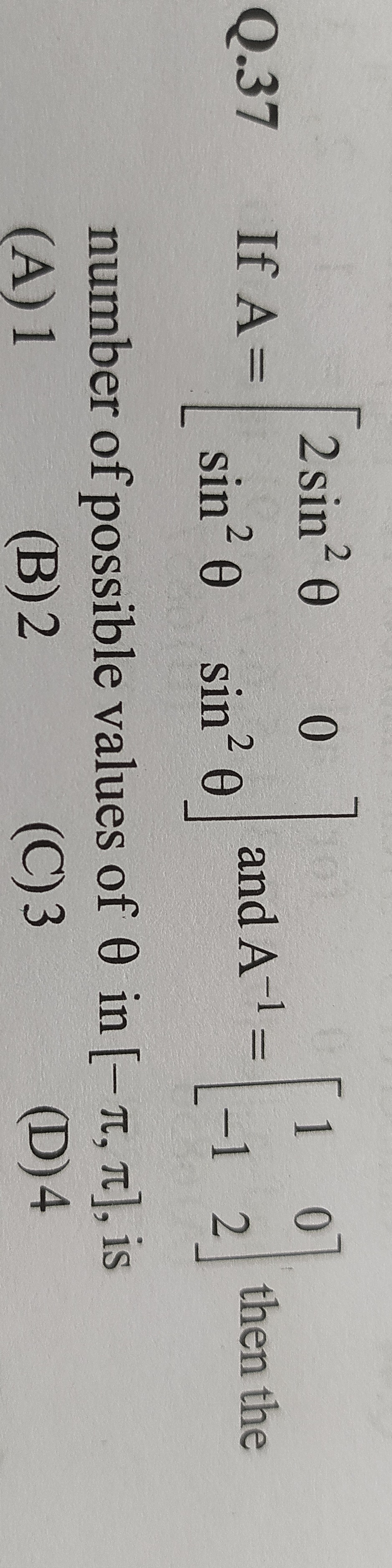
1
2
3
4
4
Solution
The given matrix is A=[2sin2θsin2θ0sin2θ]. The inverse of a 2×2 matrix M=[acbd] is M−1=det(M)1[d−c−ba], where det(M)=ad−bc. For the given matrix A, a=2sin2θ, b=0, c=sin2θ, d=sin2θ.
The determinant of A is det(A)=(2sin2θ)(sin2θ)−(0)(sin2θ)=2sin4θ. For the inverse A−1 to exist, det(A)=0, which means 2sin4θ=0, so sinθ=0.
The inverse of A is A−1=2sin4θ1[sin2θ−sin2θ−02sin2θ]=2sin4θ1[sin2θ−sin2θ02sin2θ]. Since sinθ=0, sin2θ=0. We can factor out sin2θ from the matrix: A−1=2sin4θsin2θ[1−102]=2sin2θ1[1−102].
We are given that A−1=[1−102]. Comparing the calculated inverse with the given inverse, we have: 2sin2θ1[1−102]=[1−102]. This equality holds if and only if the scalar factor is equal to 1: 2sin2θ1=1. 2sin2θ=1. sin2θ=21. Taking the square root, we get sinθ=±21.
We need to find the number of possible values of θ in the interval [−π,π] that satisfy sinθ=21 or sinθ=−21. Also, we must ensure that sinθ=0 for these values, which is true for ±21.
Case 1: sinθ=21. In the interval [−π,π], the values of θ for which sinθ=21 are in the first and second quadrants. The principal value is 4π. The solutions in [−π,π] are θ=4π (first quadrant) and θ=π−4π=43π (second quadrant). Both 4π and 43π are in [−π,π]. There are 2 solutions.
Case 2: sinθ=−21. In the interval [−π,π], the values of θ for which sinθ=−21 are in the third and fourth quadrants. The reference angle is 4π. The solutions in [−π,π] can be found by considering angles in the negative direction from 0. The angle in the fourth quadrant is −4π. The angle in the third quadrant is −π+4π=−43π. Both −4π and −43π are in [−π,π]. There are 2 solutions.
The possible values of θ in [−π,π] are 4π,43π,−4π,−43π. These are 4 distinct values. For all these values, sinθ=±21=0, so the inverse exists.
The total number of possible values of θ in [−π,π] is 2+2=4.
