Question
Question: P.T. $\pi/2 < \int_{0}^{1} \frac{dx}{\sqrt{1-x^{3/2}}} < 2$....
P.T. π/2<∫011−x3/2dx<2.
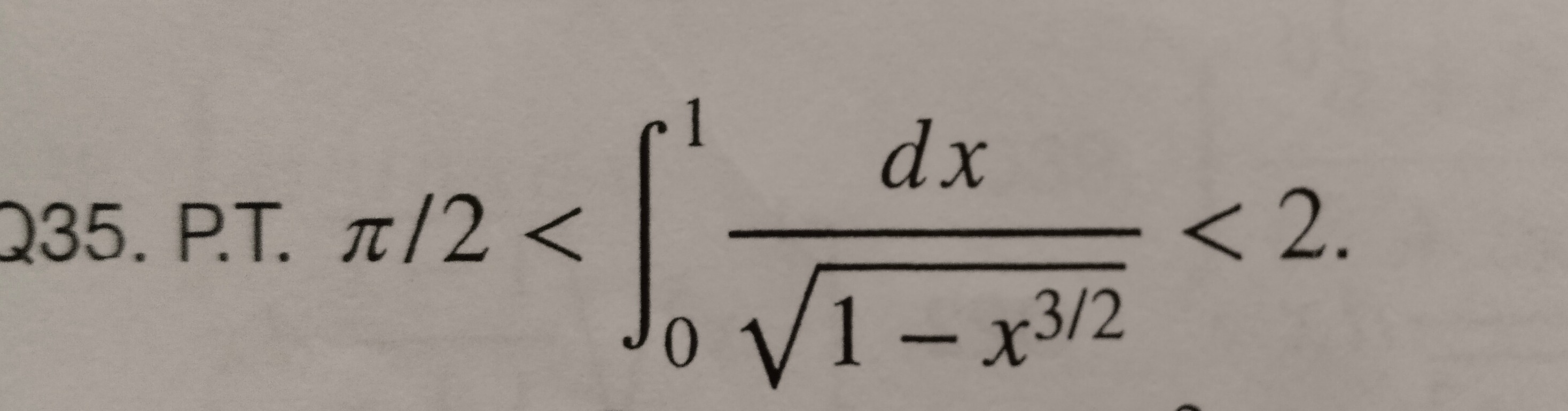
Answer
The statement 2π<∫011−x3/2dx<2 is true.
Explanation
Solution
- Lower Bound: For x∈(0,1), establish x2<x3/2. This implies 1−x2>1−x3/2. Consequently, 1−x21<1−x3/21. Integrating from 0 to 1 yields ∫011−x2dx<∫011−x3/2dx. Since ∫011−x2dx=2π, we get 2π<∫011−x3/2dx.
- Upper Bound: Use the substitution x=sin2θ, so dx=2sinθcosθdθ. The integral transforms to ∫0π/21−sin3θ2sinθcosθdθ. For θ∈(0,π/2), establish sin3θ<sin2θ. This implies 1−sin3θ>1−sin2θ=cos2θ. Thus, 1−sin3θ>cosθ, leading to 1−sin3θ1<cosθ1. Multiplying by 2sinθcosθ and integrating from 0 to π/2 yields ∫0π/21−sin3θ2sinθcosθdθ<∫0π/22sinθdθ=2. Therefore, ∫011−x3/2dx<2.
