Question
Question: Let the given polynomial be $P(x) = x^4 - 3x + 9$. The roots of $P(x)=0$ are $\alpha, \beta, \gamma,...
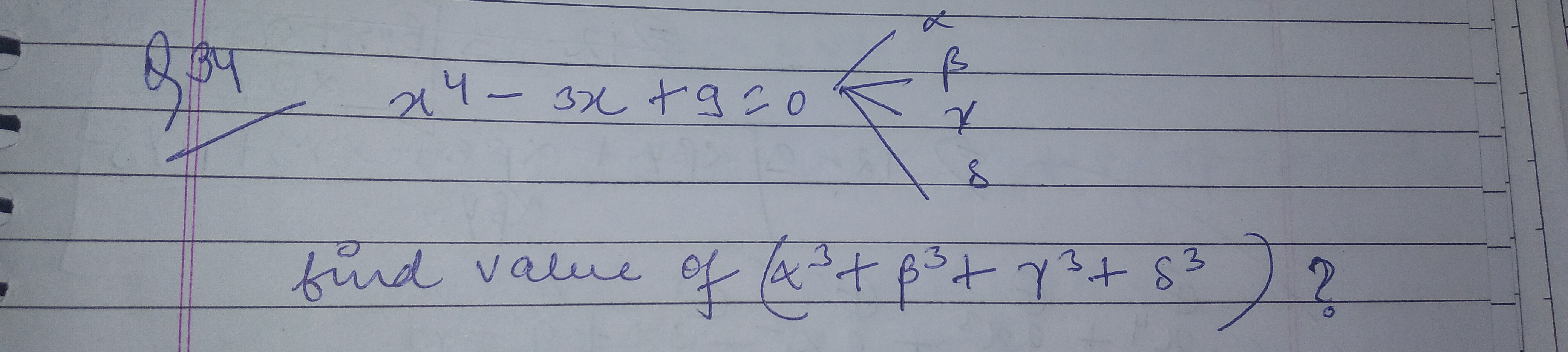
Let the given polynomial be P(x)=x4−3x+9. The roots of P(x)=0 are α,β,γ,δ. Find the value of (α3+β3+γ3+δ3).
Answer
9
Explanation
Solution
The equation is x4+0x3+0x2−3x+9=0. From Vieta's formulas: e1=∑α=0 e2=∑αβ=0 e3=∑αβγ=−(−3)/1=3 e4=αβγδ=9 Using Newton's sums: p1=e1=0 p2=e1p1−2e2=0(0)−2(0)=0 p3=e1p2−e2p1+3e3=0(0)−0(0)+3(3)=9 Thus, α3+β3+γ3+δ3=9.
