Question

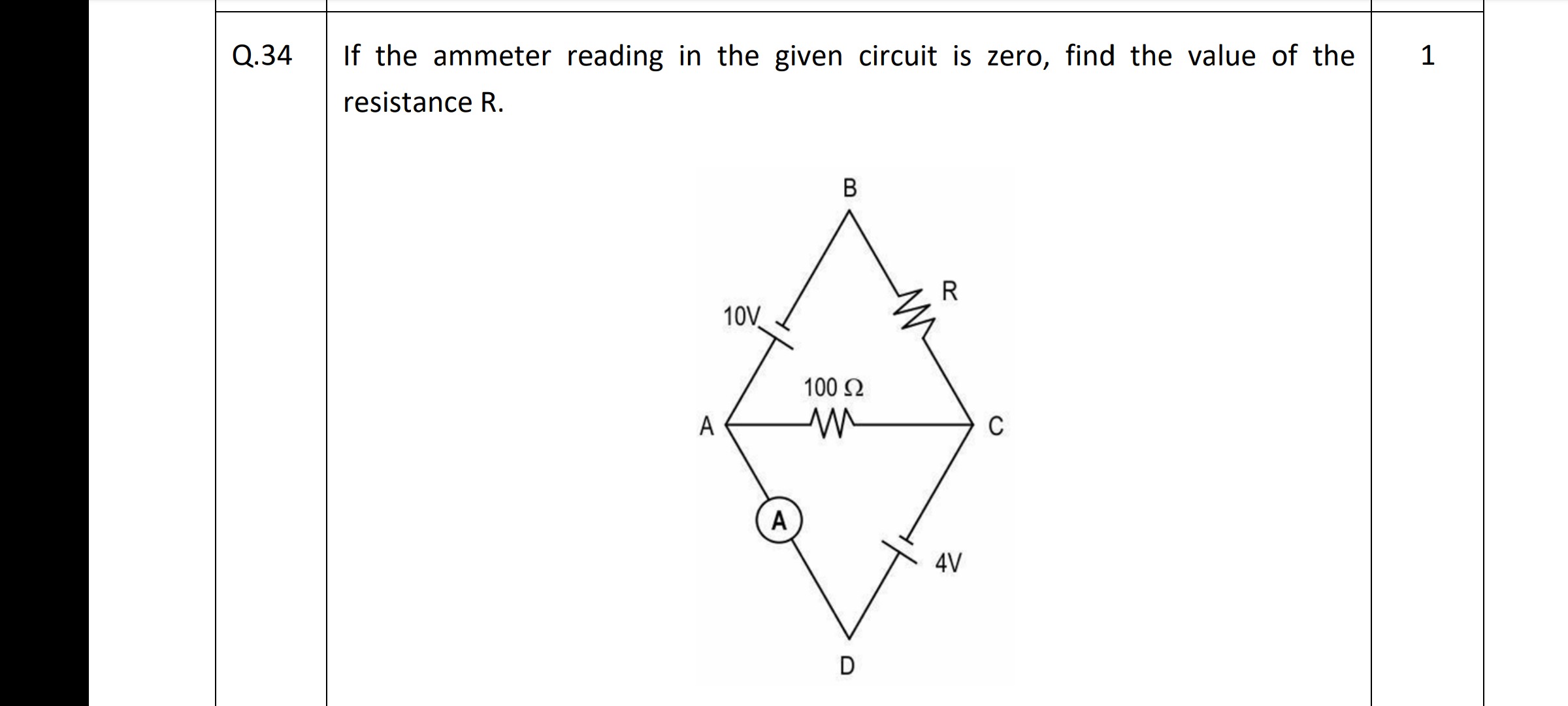
If the ammeter reading in the given circuit is zero, find the value of the resistance R. 1

Answer 1

150 \Omega

Answer 2

The problem asks us to find the value of resistance R in the given circuit, assuming the ammeter reading is zero.

1. Assign Potentials: Let's choose point D as the reference potential, so $V_D = 0$ V. Since the ammeter reading is zero, it means no current flows through the branch AD. For current to be zero in a resistive path, the potential difference across it must be zero. Therefore, $V_A = V_D = 0$ V.

2. Determine Potentials of B and C:

• Branch AB: There is a 10V voltage source between A and B. The positive terminal (longer line) is towards B, and the negative terminal (shorter line) is towards A. This means $V_B - V_A = 10$ V. Since $V_A = 0$ V, we have $V_B - 0 = 10$ V, so $V_B = 10$ V.
• Branch CD: There is a 4V voltage source between C and D. The positive terminal is towards C, and the negative terminal is towards D. This means $V_C - V_D = 4$ V. Since $V_D = 0$ V, we have $V_C - 0 = 4$ V, so $V_C = 4$ V.

Now we have the potentials of all four nodes: $V_A = 0$ V $V_B = 10$ V $V_C = 4$ V $V_D = 0$ V

3. Calculate Currents in Resistive Branches:

• Current through 100 Ω resistor (branch AC): The potential difference across the 100 Ω resistor is $V_{CA} = V_C - V_A = 4 - 0 = 4$ V. The current flowing from C to A, $I_{CA} = \frac{V_C - V_A}{100 \, \Omega} = \frac{4 \, \text{V}}{100 \, \Omega} = 0.04$ A.

• Current through R (branch BC): The potential difference across resistance R is $V_{BC} = V_B - V_C = 10 - 4 = 6$ V. The current flowing from B to C, $I_{BC} = \frac{V_B - V_C}{R} = \frac{6 \, \text{V}}{R}$.

4. Apply Kirchhoff's Current Law (KCL): Let's apply KCL at node A. Currents entering node A = Currents leaving node A.

• Current from C to A is $I_{CA} = 0.04$ A.
• Current from D to A through the ammeter is $I_{DA} = 0$ A (given).
• Let $I_{AB}$ be the current flowing from A to B through the 10V source.

KCL at node A: $I_{CA} + I_{DA} = I_{AB}$ $0.04 \, \text{A} + 0 \, \text{A} = I_{AB}$ So, $I_{AB} = 0.04$ A.

Now, let's apply KCL at node B.

• Current entering node B from A is $I_{AB} = 0.04$ A.
• Current leaving node B towards C is $I_{BC}$.

KCL at node B: $I_{AB} = I_{BC}$ So, $I_{BC} = 0.04$ A.

5. Solve for R: We have two expressions for $I_{BC}$:

1. $I_{BC} = 6/R$
2. $I_{BC} = 0.04$ A

Equating these two expressions: $\frac{6}{R} = 0.04$ $R = \frac{6}{0.04} = \frac{6}{\frac{4}{100}} = \frac{6 \times 100}{4} = \frac{600}{4}$ $R = 150 \, \Omega$

Verification (Optional): Let's check KCL at node C. Current entering C: $I_{BC} = 0.04$ A. Current leaving C: $I_{CA} = 0.04$ A. Let $I_{CD}$ be the current flowing from C to D through the 4V source. KCL at C: $I_{BC} = I_{CA} + I_{CD}$ $0.04 = 0.04 + I_{CD}$ This implies $I_{CD} = 0$. This means no current flows through the 4V source, which is consistent with the potentials ($V_C - V_D = 4-0 = 4$ V) and the rest of the circuit's current distribution.