Solveeit Logo
Login

Question

Question: Find $\frac{\sum \alpha^3}{\sum x^2}$ for the equation $x^3 + ax + b = 0$....

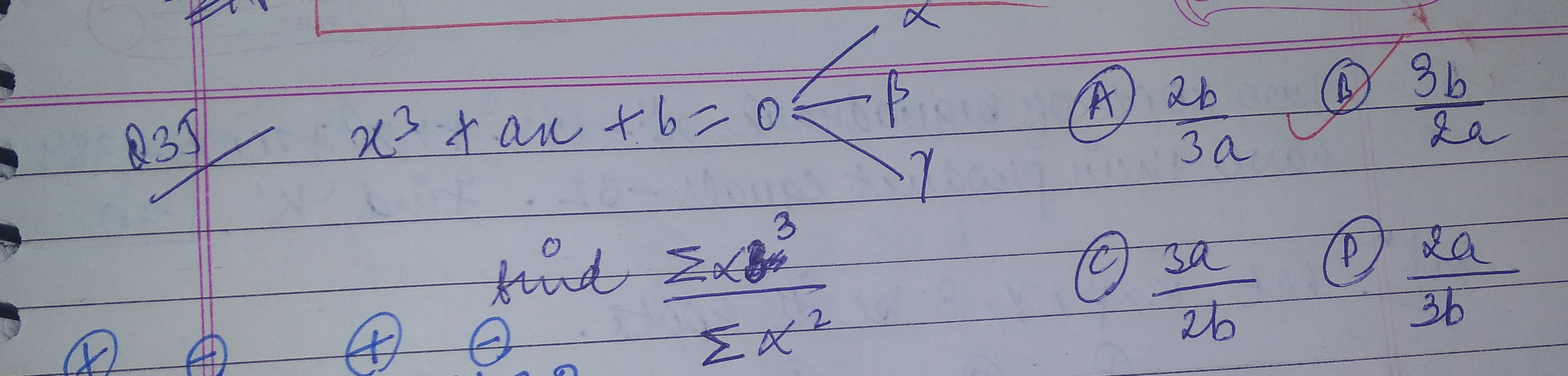
Find ∑α3∑x2\frac{\sum \alpha^3}{\sum x^2} for the equation x3+ax+b=0x^3 + ax + b = 0.

A

2b3a\frac{2b}{3a}

B

3b2a\frac{3b}{2a}

C

3a2b\frac{3a}{2b}

D

2a3b\frac{2a}{3b}

Answer

3b2a\frac{3b}{2a}

Explanation

Solution

Let the roots of x3+ax+b=0x^3 + ax + b = 0 be α,β,γ\alpha, \beta, \gamma. From Vieta's formulas:

  1. α+β+γ=0\alpha + \beta + \gamma = 0
  2. αβ+βγ+γα=a\alpha\beta + \beta\gamma + \gamma\alpha = a
  3. αβγ=−b\alpha\beta\gamma = -b

We need to find ∑α3∑α2\frac{\sum \alpha^3}{\sum \alpha^2}.

For ∑α2\sum \alpha^2: ∑α2=(α+β+γ)2−2(αβ+βγ+γα)\sum \alpha^2 = (\alpha + \beta + \gamma)^2 - 2(\alpha\beta + \beta\gamma + \gamma\alpha) ∑α2=(0)2−2(a)=−2a\sum \alpha^2 = (0)^2 - 2(a) = -2a

For ∑α3\sum \alpha^3: Since α\alpha is a root, α3+aα+b=0  ⟹  α3=−aα−b\alpha^3 + a\alpha + b = 0 \implies \alpha^3 = -a\alpha - b. Similarly, β3=−aβ−b\beta^3 = -a\beta - b and γ3=−aγ−b\gamma^3 = -a\gamma - b. Summing these: ∑α3=−a(α+β+γ)−3b\sum \alpha^3 = -a(\alpha + \beta + \gamma) - 3b ∑α3=−a(0)−3b=−3b\sum \alpha^3 = -a(0) - 3b = -3b

The ratio is ∑α3∑α2=−3b−2a=3b2a\frac{\sum \alpha^3}{\sum \alpha^2} = \frac{-3b}{-2a} = \frac{3b}{2a}.