Question

If $p \in (0,1)$ such that

$k = sgn(101p^{50}(1 - p) - 1 + p^{101})$ and $\ell_n = \sum_{r=1}^{n-1}\frac{2r^2 + kr(n-2) + 1}{(n-r){n \choose r}}$,

then $15\ell_{15} - k$ is equal to

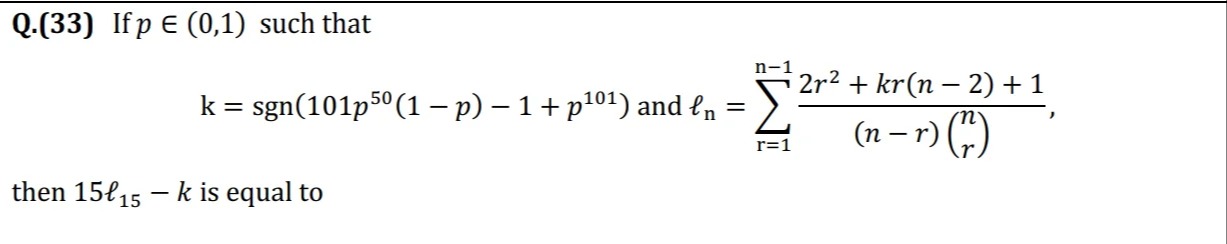
Answer 1

225

Answer 2

Solution Explanation

1. We first note that   $k = \operatorname{sgn}\Big(101\,p^{50}(1-p) - 1 + p^{101}\Big).$ Since $p\in (0,1)$, one verifies that   $101\,p^{50}(1-p)+p^{101} < 1,$ so the expression inside the sign function is negative. Hence,
     $k = -1.$

2. With $k=-1$, the sum becomes
     $$ \ell_n = \sum_{r=1}^{n-1} \frac{2r^2 - r(n-2) + 1}{(n-r){n \choose r}}.

By evaluating for small values of $n$ (for example, $n=2,3,4,5$) one finds:   - For $n=2$: $\ell_2=\frac{3}{2}=\frac{2^2-1}{2}$,   - For $n=3$: $\ell_3=\frac{8}{3}=\frac{3^2-1}{3}$,   - For $n=4$: $\ell_4=\frac{15}{4}=\frac{4^2-1}{4}$,   - For $n=5$: $\ell_5=\frac{24}{5}=\frac{5^2-1}{5}$. This suggests the general result:   $$ \ell_n = \frac{n^2-1}{n}.

3. For $n=15$,   $$ \ell_{15} = \frac{15^2-1}{15} = \frac{225-1}{15} = \frac{224}{15}.

Thus,   $$ 15\ell_{15} - k = 15\cdot\frac{224}{15} - (-1) = 224 + 1 = 225.