Solveeit Logo
Login

Question

Question: If the lines x+ay+a=0, bx+y+b=0, cx+cy+1=0, where a, b, c are non-zero and non-unity, pass through...

If the lines

x+ay+a=0, bx+y+b=0, cx+cy+1=0,

where a, b, c are non-zero and non-unity, pass through the same point then the value of

a1−a+b1−b+c1−c\frac{a}{1-a} + \frac{b}{1-b} + \frac{c}{1-c} is equal to

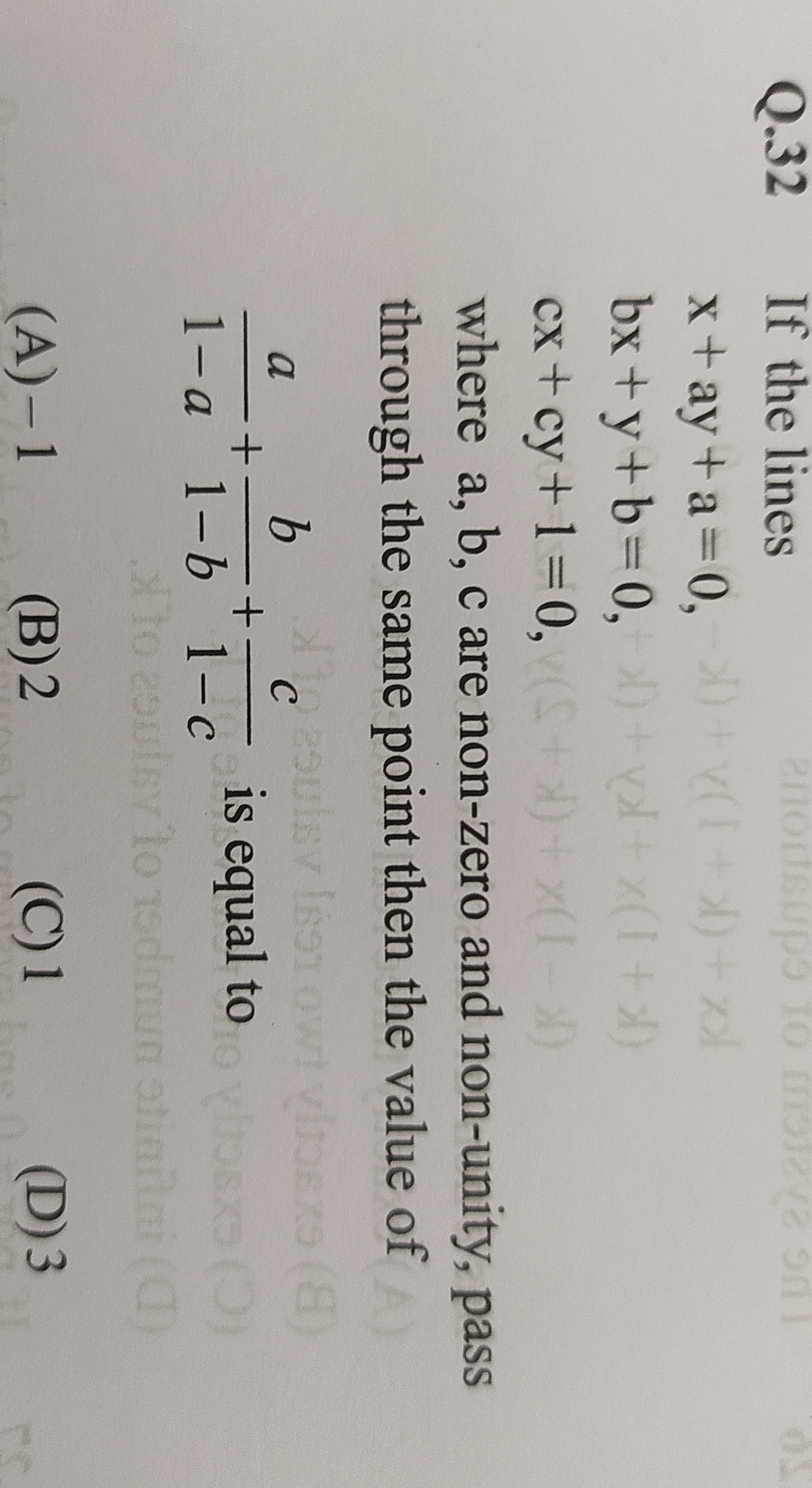
A

-1

B

2

C

1

D

3

Answer

-1

Explanation

Solution

Given the lines

L1:x+ay+a=0,L2:bx+y+b=0,L3:cx+cy+1=0,L_1: x + ay + a=0,\quad L_2: bx + y + b=0,\quad L_3: cx + cy + 1=0,

concurrent at a point, their coefficients (in homogeneous form) must satisfy the determinant condition:

∣1aab1bcc1∣=0.\begin{vmatrix} 1 & a & a \\ b & 1 & b \\ c & c & 1 \end{vmatrix} = 0.

Expanding the determinant along the first row:

1∣1bc1∣−a∣bbc1∣+a∣b1cc∣=0.1\begin{vmatrix}1&b\\ c&1\end{vmatrix} - a\begin{vmatrix}b&b\\ c&1\end{vmatrix} + a\begin{vmatrix}b&1\\ c&c\end{vmatrix} = 0.

Calculating the 2×2 determinants:

∣1bc1∣=1−bc,∣bbc1∣=b(1−c),∣b1cc∣=c(b−1).\begin{vmatrix}1&b\\ c&1\end{vmatrix} = 1-bc,\quad \begin{vmatrix}b&b\\ c&1\end{vmatrix} = b(1-c),\quad \begin{vmatrix}b&1\\ c&c\end{vmatrix} = c(b-1).

Thus, the condition becomes:

1−bc−a b(1−c)+a c(b−1)=0.1-bc - a\,b(1-c) + a\,c(b-1) = 0.

Rearrange to express aa:

1−bc+a[−b(1−c)+c(b−1)]=0.1 - bc + a\big[-b(1-c)+ c(b-1)\big]= 0.

Note that:

−b(1−c)+c(b−1)=−b+bc+cb−c=2bc−b−c.-b(1-c)+ c(b-1) = -b+bc+cb-c = 2bc - b - c.

Thus,

1−bc+a(2bc−b−c)=0⟹a=bc−12bc−b−c.1-bc + a(2bc-b-c)=0 \quad\Longrightarrow\quad a = \frac{bc-1}{2bc-b-c}.

Now, we need to evaluate:

S=a1−a+b1−b+c1−c.S = \frac{a}{1-a} + \frac{b}{1-b} + \frac{c}{1-c}.

Compute a1−a\frac{a}{1-a}:

Given a=bc−12bc−b−ca = \frac{bc-1}{2bc-b-c}, then

1−a=1−bc−12bc−b−c=(2bc−b−c)−(bc−1)2bc−b−c=bc−b−c+12bc−b−c.1-a = 1 - \frac{bc-1}{2bc-b-c} = \frac{(2bc-b-c) - (bc-1)}{2bc-b-c} = \frac{bc - b - c + 1}{2bc-b-c}.

Recognize that:

bc−b−c+1=(b−1)(c−1).bc - b - c + 1 = (b-1)(c-1).

Thus,

a1−a=bc−12bc−b−c(b−1)(c−1)2bc−b−c=bc−1(b−1)(c−1).\frac{a}{1-a} = \frac{\frac{bc-1}{2bc-b-c}}{\frac{(b-1)(c-1)}{2bc-b-c}} = \frac{bc-1}{(b-1)(c-1)}.

Also observe:

b1−b=−bb−1,c1−c=−cc−1.\frac{b}{1-b} = -\frac{b}{b-1}, \quad \frac{c}{1-c} = -\frac{c}{c-1}.

So,

S=bc−1(b−1)(c−1)−bb−1−cc−1.S = \frac{bc-1}{(b-1)(c-1)} - \frac{b}{b-1} - \frac{c}{c-1}.

Get a common denominator (b−1)(c−1)(b-1)(c-1) for the last two terms:

bb−1=b(c−1)(b−1)(c−1),cc−1=c(b−1)(b−1)(c−1).\frac{b}{b-1} = \frac{b(c-1)}{(b-1)(c-1)},\quad \frac{c}{c-1} = \frac{c(b-1)}{(b-1)(c-1)}.

Thus,

S=bc−1−b(c−1)−c(b−1)(b−1)(c−1).S = \frac{bc-1 - b(c-1) - c(b-1)}{(b-1)(c-1)}.

Expanding the numerator:

bc−1−[bc−b]−[bc−c]=bc−1−bc+b−bc+c=b+c−1−bc.bc-1 - \big[bc - b\big] - \big[bc - c\big] = bc-1 - bc + b - bc + c = b+c -1 -bc.

Notice that:

b+c−1−bc=−(1−b−c+bc)=−(1−b)(1−c).b+c -1 - bc = -(1-b-c+bc) = -(1-b)(1-c).

Also, note that:

(b−1)(c−1)=(−(1−b))⋅(−(1−c))=(1−b)(1−c).(b-1)(c-1) = (-(1-b))\cdot (-(1-c)) = (1-b)(1-c).

Finally,

S=−(1−b)(1−c)(1−b)(1−c)=−1.S = \frac{- (1-b)(1-c)}{(1-b)(1-c)} = -1.

So, the value is −1-1.