Question
Question: If x = f(t) & y = g(t) are diff f^n of t so that y is diff f^n of x & $\frac{dx}{dt} \neq 0$ then PT...
If x = f(t) & y = g(t) are diff f^n of t so that y is diff f^n of x & dtdx=0 then PT dxdy=dx/dtdy/dt Hence find dxdy if x = sint & y = cost
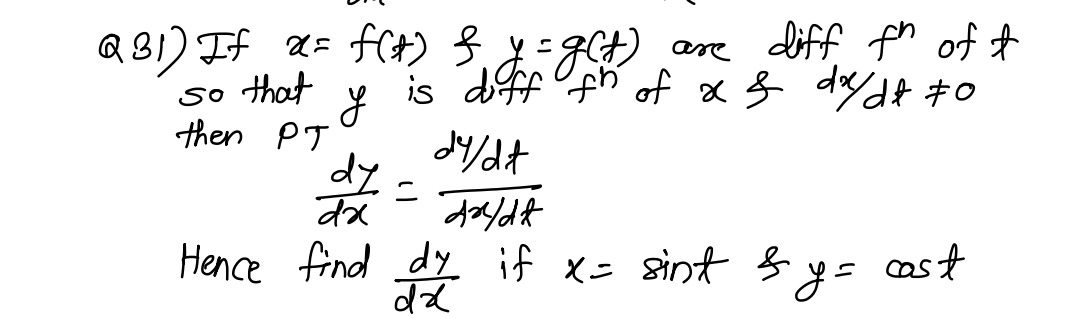
dxdy=−tant
Solution
Here's the solution to the problem:
Part 1: Proof
Given that x=f(t) and y=g(t) are differentiable functions of t, and y is a differentiable function of x. We are also given that dtdx=0.
Since y is a differentiable function of x, and x is a differentiable function of t, by the chain rule for functions of a single variable, we have: dtdy=dxdy⋅dtdx Given that dtdx=0, we can divide both sides of the equation by dtdx: dx/dtdy/dt=dxdy Rearranging the terms, we get: dxdy=dx/dtdy/dt This proves the required formula for the derivative of parametric functions.
Part 2: Application
Given the parametric equations: x=sint y=cost
We need to find dxdy. First, we find the derivatives of x and y with respect to t: dtdx=dtd(sint)=cost dtdy=dtd(cost)=−sint Now, using the formula dxdy=dx/dtdy/dt (assuming dtdx=cost=0): dxdy=cost−sint dxdy=−tant
Thus, if x=sint and y=cost, then dxdy=−tant.
