Question

$\sum_{0 \leq i \leq j \leq 10} ({^{10}C_i}) ({^{i}C_j})$ is equal to

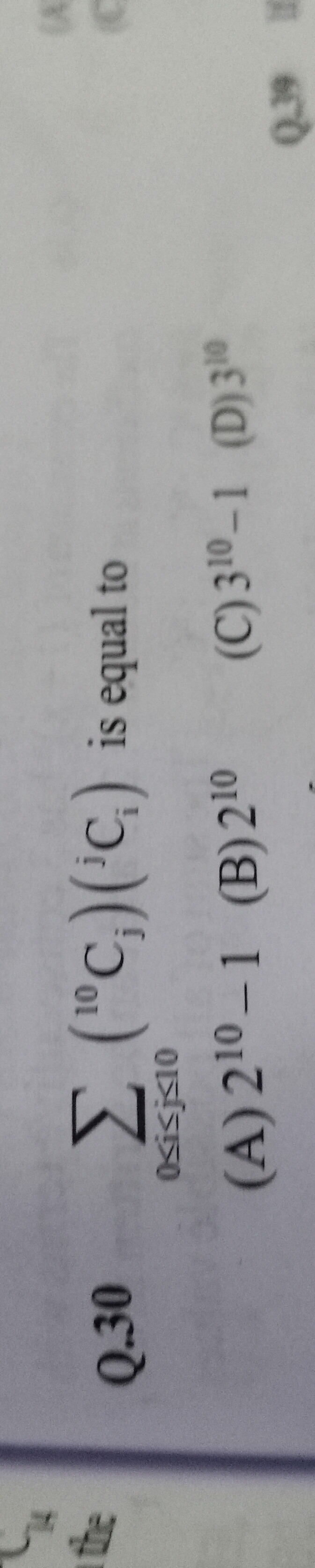
• A. $2^{10}-1$
• B. $2^{10}$
• C. $3^{10}-1$
• D. $3^{10}$

Answer 1

Answer: (B)

$2^{10}$

Answer 2

The term ${^{i}C_j}$ is non-zero only if $j \leq i$. The summation is over $0 \leq i \leq j \leq 10$. For a term ${^{10}C_i} {^{i}C_j}$ to be non-zero, we must satisfy both $i \leq j$ (from summation limits) and $j \leq i$ (for ${^{i}C_j}$ to be non-zero). This implies $i=j$. Thus, the sum reduces to $\sum_{i=0}^{10} {^{10}C_i} {^{i}C_i} = \sum_{i=0}^{10} {^{10}C_i} \times 1 = \sum_{i=0}^{10} {^{10}C_i} = 2^{10}$.