Question
Question: $(x-3)^2 + |x-3| - 11 = 0$ the sum of solutions of equation is...
(x−3)2+∣x−3∣−11=0 the sum of solutions of equation is
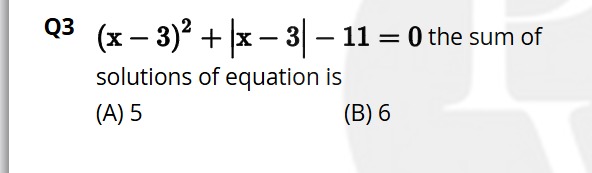
5
6
6
Solution
The given equation is (x−3)2+∣x−3∣−11=0. We can notice that (x−3)2=∣x−3∣2. Let y=∣x−3∣. Since ∣x−3∣ represents an absolute value, y≥0. Substituting y into the equation, we get: y2+y−11=0
This is a quadratic equation in y. We can solve for y using the quadratic formula y=2a−b±b2−4ac, where a=1, b=1, c=−11. y=2(1)−1±12−4(1)(−11) y=2−1±1+44 y=2−1±45 y=2−1±35
We have two possible values for y: y1=2−1+35 y2=2−1−35
Since y=∣x−3∣, y must be non-negative (y≥0). We only consider the valid solution for y:
∣x−3∣=2−1+35
Since the right side 2−1+35 is positive, the equation ∣x−3∣=k where k>0 has two solutions: x−3=k and x−3=−k. Here, k=2−1+35.
Case 1: x−3=2−1+35 x1=3+2−1+35=26+2−1+35=26−1+35=25+35
Case 2: x−3=−(2−1+35) x−3=21−35 x2=3+21−35=26+21−35=26+1−35=27−35
The solutions of the equation are x1=25+35 and x2=27−35.
The question asks for the sum of the solutions. Sum of solutions =x1+x2 Sum =25+35+27−35 Sum =2(5+35)+(7−35) Sum =25+35+7−35 Sum =212+(35−35) Sum =212+0 Sum =212 Sum =6
The sum of the solutions is 6.
