Question
Question: The letters of the word LOGARITHM are arranged at random, the probability that exactly 4 letters are...
The letters of the word LOGARITHM are arranged at random, the probability that exactly 4 letters are between G and H is
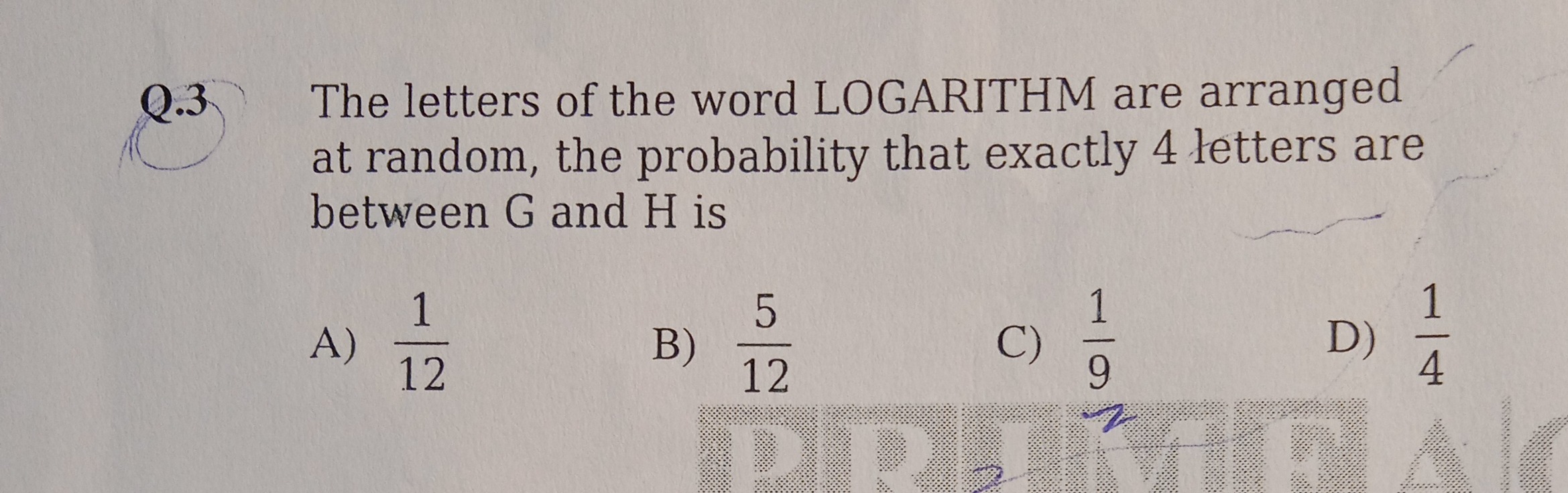
121
125
91
41
91
Solution
The problem asks for the probability that exactly 4 letters are between G and H when the letters of the word LOGARITHM are arranged at random.
1. Total number of arrangements:
The word LOGARITHM has 9 distinct letters. The total number of ways to arrange these 9 distinct letters is 9!.
Total arrangements = 9!=362,880.
2. Number of favorable arrangements:
We want exactly 4 letters to be between G and H.
-
Step 1: Identify the number of possible positions for the block (G _ _ _ _ H).
Let N be the total number of letters (9). Let k be the number of letters between G and H (4). The block (G _ _ _ _ H) has k+2=4+2=6 letters. The number of possible starting positions for G (or H) such that there are 4 letters between them is N−(k+1)=9−(4+1)=9−5=4. These are (G at 1, H at 6), (G at 2, H at 7), (G at 3, H at 8), (G at 4, H at 9). So, 4 pairs of positions.
-
Step 2: Arrange G and H.
For each pair of positions, G and H can be arranged in 2! ways.
-
Step 3: Arrange the remaining letters.
The remaining (N−2) letters (7 letters) can be arranged in the remaining (N−2) positions (7 positions) in 7! ways.
Favorable arrangements = (Number of position pairs) × (Arrangement of G and H) × (Arrangement of remaining letters)
Favorable arrangements = 4×2!×7!
Favorable arrangements = 4×2×5040=8×5040=40,320.
3. Calculate the probability:
Probability = (Favorable arrangements) / (Total arrangements)
Probability = 9!4×2!×7!
Probability = 9×8×7!4×2×7!
Probability = 9×84×2
Probability = 728
Probability = 91
