Question

The length of the perpendicular from the point$(a, 4, 2), a > 0$ to the line $\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}$ is $2\sqrt{6}$ and $Q(\alpha_1, \alpha_2, \alpha_3)$ is the image of a point $P$ in the line then $a + \alpha_1 + \alpha_2 + \alpha_3$ is equal to

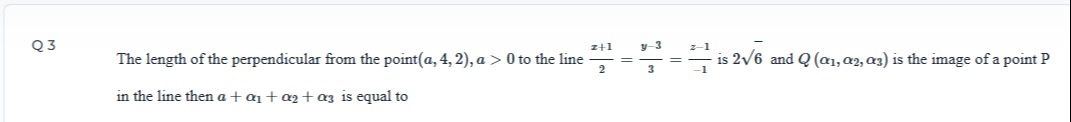
• A. 5
• B. 8
• C. 12
• D. 14

Answer 1

Answer: (B)

8

Answer 2

Let the given point be $P = (a, 4, 2)$ with $a > 0$. The given line is $L: \frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}$. The direction ratios of the line are $(2, 3, -1)$. Let $R$ be the foot of the perpendicular from $P$ to the line $L$. A general point on the line $L$ can be written as $R = (-1 + 2\lambda, 3 + 3\lambda, 1 - \lambda)$ for some scalar $\lambda$.

The vector $\vec{PR}$ is given by $R - P = (-1 + 2\lambda - a, 3 + 3\lambda - 4, 1 - \lambda - 2) = (-1 - a + 2\lambda, -1 + 3\lambda, -1 - \lambda)$. Since $\vec{PR}$ is perpendicular to the direction vector of the line $(2, 3, -1)$, their dot product is zero: $\vec{PR} \cdot (2, 3, -1) = 2(-1 - a + 2\lambda) + 3(-1 + 3\lambda) - 1(-1 - \lambda) = 0$ $-2 - 2a + 4\lambda - 3 + 9\lambda + 1 + \lambda = 0$ $14\lambda - 2a - 4 = 0$ $7\lambda - a - 2 = 0 \implies \lambda = \frac{a+2}{7}$.

The length of the perpendicular $PR$ is given as $2\sqrt{6}$, so $PR^2 = (2\sqrt{6})^2 = 24$. $PR^2 = (-1 - a + 2\lambda)^2 + (-1 + 3\lambda)^2 + (-1 - \lambda)^2 = 24$.

Substitute $\lambda = \frac{a+2}{7}$ into the components of $\vec{PR}$: $x$-component: $-1 - a + 2\left(\frac{a+2}{7}\right) = \frac{-7 - 7a + 2a + 4}{7} = \frac{-5a - 3}{7}$ $y$-component: $-1 + 3\left(\frac{a+2}{7}\right) = \frac{-7 + 3a + 6}{7} = \frac{3a - 1}{7}$ $z$-component: $-1 - \left(\frac{a+2}{7}\right) = \frac{-7 - a - 2}{7} = \frac{-a - 9}{7}$

Now substitute these into the $PR^2$ equation: $\left(\frac{-5a - 3}{7}\right)^2 + \left(\frac{3a - 1}{7}\right)^2 + \left(\frac{-a - 9}{7}\right)^2 = 24$ $\frac{1}{49} [ (25a^2 + 30a + 9) + (9a^2 - 6a + 1) + (a^2 + 18a + 81) ] = 24$ $35a^2 + 42a + 91 = 24 \times 49 = 1176$ $35a^2 + 42a - 1085 = 0$ Dividing by 7, we get: $5a^2 + 6a - 155 = 0$. Factoring this quadratic equation: $(5a+31)(a-5) = 0$. The possible values for $a$ are $a=5$ or $a=-31/5$. Since $a > 0$, we have $a=5$.

Now we find the value of $\lambda$ using $a=5$: $\lambda = \frac{a+2}{7} = \frac{5+2}{7} = 1$.

The coordinates of the foot of the perpendicular $R$ are: $R = (-1 + 2\lambda, 3 + 3\lambda, 1 - \lambda) = (-1 + 2(1), 3 + 3(1), 1 - 1) = (1, 6, 0)$.

The point $Q(\alpha_1, \alpha_2, \alpha_3)$ is the image of $P(a, 4, 2)$ in the line $L$. The foot of the perpendicular $R$ is the midpoint of the segment $PQ$. So, $R = \left(\frac{a + \alpha_1}{2}, \frac{4 + \alpha_2}{2}, \frac{2 + \alpha_3}{2}\right)$. Using $P=(5, 4, 2)$ and $R=(1, 6, 0)$: $1 = \frac{5 + \alpha_1}{2} \implies 2 = 5 + \alpha_1 \implies \alpha_1 = -3$. $6 = \frac{4 + \alpha_2}{2} \implies 12 = 4 + \alpha_2 \implies \alpha_2 = 8$. $0 = \frac{2 + \alpha_3}{2} \implies 0 = 2 + \alpha_3 \implies \alpha_3 = -2$. Thus, $Q = (-3, 8, -2)$.

We need to find the value of $a + \alpha_1 + \alpha_2 + \alpha_3$. $a + \alpha_1 + \alpha_2 + \alpha_3 = 5 + (-3) + 8 + (-2) = 5 - 3 + 8 - 2 = 8$.