Solveeit Logo
Login

Question

Question: Let $\vec{a} = 3\hat{i} - \hat{j} + 2\hat{k}$ and $\vec{b} = \vec{a} \times (\hat{i} - 2\hat{k})$ an...

Let a⃗=3i^−j^+2k^\vec{a} = 3\hat{i} - \hat{j} + 2\hat{k} and b⃗=a⃗×(i^−2k^)\vec{b} = \vec{a} \times (\hat{i} - 2\hat{k}) and c⃗=b⃗×k^\vec{c} = \vec{b} \times \hat{k} then projection of a⃗\vec{a} on c⃗+2j^\vec{c}+2\hat{j}

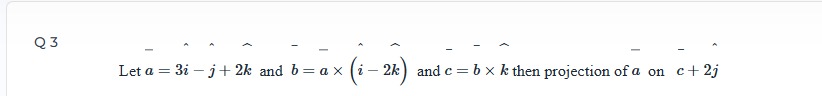
Answer

3i^3\hat{i}

Explanation

Solution

Steps:

  1. Calculate b⃗\vec{b}: Given a⃗=3i^−j^+2k^\vec{a} = 3\hat{i} - \hat{j} + 2\hat{k} and let v⃗=i^−2k^\vec{v} = \hat{i} - 2\hat{k}.

    b⃗=a⃗×v⃗=(3i^−j^+2k^)×(i^−2k^)\vec{b} = \vec{a} \times \vec{v} = (3\hat{i} - \hat{j} + 2\hat{k}) \times (\hat{i} - 2\hat{k})

    Using the determinant method for cross product:

    b⃗=∣i^j^k^3−1210−2∣=i^((−1)(−2)−(2)(0))−j^((3)(−2)−(2)(1))+k^((3)(0)−(−1)(1))\vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -1 & 2 \\ 1 & 0 & -2 \end{vmatrix} = \hat{i}((-1)(-2) - (2)(0)) - \hat{j}((3)(-2) - (2)(1)) + \hat{k}((3)(0) - (-1)(1)) b⃗=i^(2)−j^(−6−2)+k^(1)=2i^+8j^+k^\vec{b} = \hat{i}(2) - \hat{j}(-6 - 2) + \hat{k}(1) = 2\hat{i} + 8\hat{j} + \hat{k}

  2. Calculate c⃗\vec{c}:

    c⃗=b⃗×k^=(2i^+8j^+k^)×k^\vec{c} = \vec{b} \times \hat{k} = (2\hat{i} + 8\hat{j} + \hat{k}) \times \hat{k}

    Using the properties of cross products of unit vectors (i^×k^=−j^\hat{i} \times \hat{k} = -\hat{j}, j^×k^=i^\hat{j} \times \hat{k} = \hat{i}, k^×k^=0⃗\hat{k} \times \hat{k} = \vec{0}):

    c⃗=(2i^×k^)+(8j^×k^)+(k^×k^)\vec{c} = (2\hat{i} \times \hat{k}) + (8\hat{j} \times \hat{k}) + (\hat{k} \times \hat{k}) c⃗=2(−j^)+8(i^)+0⃗=8i^−2j^\vec{c} = 2(-\hat{j}) + 8(\hat{i}) + \vec{0} = 8\hat{i} - 2\hat{j}

  3. Calculate the vector to project on: Let d⃗=c⃗+2j^\vec{d} = \vec{c} + 2\hat{j}.

    d⃗=(8i^−2j^)+2j^=8i^\vec{d} = (8\hat{i} - 2\hat{j}) + 2\hat{j} = 8\hat{i}

  4. Calculate the projection of a⃗\vec{a} on d⃗\vec{d}: The formula for the vector projection of a⃗\vec{a} on d⃗\vec{d} is:

    projd⃗a⃗=a⃗⋅d⃗∣d⃗∣2d⃗\text{proj}_{\vec{d}} \vec{a} = \frac{\vec{a} \cdot \vec{d}}{|\vec{d}|^2} \vec{d}

    Calculate the dot product a⃗⋅d⃗\vec{a} \cdot \vec{d}:

    a⃗⋅d⃗=(3i^−j^+2k^)⋅(8i^)=(3)(8)+(−1)(0)+(2)(0)=24\vec{a} \cdot \vec{d} = (3\hat{i} - \hat{j} + 2\hat{k}) \cdot (8\hat{i}) = (3)(8) + (-1)(0) + (2)(0) = 24

    Calculate the squared magnitude of d⃗\vec{d}:

    ∣d⃗∣2=∣8i^∣2=82=64|\vec{d}|^2 = |8\hat{i}|^2 = 8^2 = 64

    Substitute these values into the projection formula:

    projd⃗a⃗=2464(8i^)=38(8i^)=3i^\text{proj}_{\vec{d}} \vec{a} = \frac{24}{64} (8\hat{i}) = \frac{3}{8} (8\hat{i}) = 3\hat{i}

The projection of a⃗\vec{a} on c⃗+2j^\vec{c}+2\hat{j} is 3i^3\hat{i}.