Question

Let $g(x) = \tan^{-1}|x| - \cot^{-1}|x|$, $f(x) = \frac{[x]}{[x+1]}\{x\}$, $h(x) = |g(f(x))|$ where $\{x\}$ denotes fractional part and $[x]$ denotes the integral part then which of the following holds good?

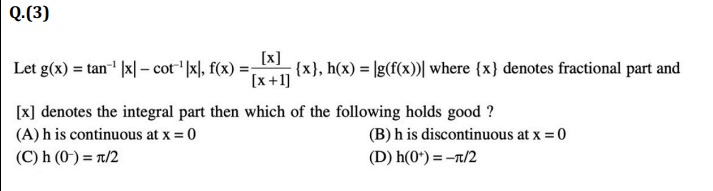
• A. h is continuous at x = 0
• B. h is discontinuous at x = 0
• C. h (0-) = $\pi/2$
• D. h(0+) = –$\pi/2$

Answer 1

Answer: (B)

B

Answer 2

The functions are given by $g(x) = \tan^{-1}|x| - \cot^{-1}|x|$, $f(x) = \frac{[x]}{[x+1]}\{x\}$, and $h(x) = |g(f(x))|$. We need to analyze the continuity of $h(x)$ at $x=0$.

First, let's simplify $g(x)$. Using the identity $\tan^{-1}y + \cot^{-1}y = \frac{\pi}{2}$, we have $\cot^{-1}|x| = \frac{\pi}{2} - \tan^{-1}|x|$. So, $g(x) = \tan^{-1}|x| - (\frac{\pi}{2} - \tan^{-1}|x|) = 2\tan^{-1}|x| - \frac{\pi}{2}$. The function $g(y) = 2\tan^{-1}|y| - \frac{\pi}{2}$ is defined and continuous for all $y \in \mathbb{R}$.

Next, let's analyze $f(x) = \frac{[x]}{[x+1]}\{x\}$ around $x=0$. The function $f(x)$ is defined only when the denominator $[x+1] \ne 0$. $[x+1] = 0$ if and only if $0 \le x+1 < 1$, which means $-1 \le x < 0$. So, the domain of $f(x)$ is $\mathbb{R} \setminus [-1, 0)$.

Let's evaluate $f(x)$ at $x=0$ and its limits as $x \to 0$. At $x=0$: $[0]=0$, $[0+1]=[1]=1$, $\{0\}=0$. $f(0) = \frac{[0]}{[0+1]}\{0\} = \frac{0}{1} \cdot 0 = 0$.

For the right-hand limit as $x \to 0^+$: Consider $x \in (0, \epsilon)$ for a small $\epsilon > 0$, e.g., $\epsilon < 1$. In this interval, $[x]=0$, $[x+1]=1$, $\{x\}=x$. $f(x) = \frac{0}{1} \cdot x = 0$. So, $\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} 0 = 0$.

For the left-hand limit as $x \to 0^-$: Consider $x \in (-\epsilon, 0)$ for a small $\epsilon > 0$. If $0 < \epsilon \le 1$, then for $x \in (-\epsilon, 0)$, we have $-1 \le x < 0$. In this interval, $[x+1]=0$. Since the denominator $[x+1]=0$ for $x \in [-1, 0)$, the function $f(x)$ is undefined for $x$ in any left neighborhood of 0 (specifically, for $x \in [-1, 0)$). Therefore, the left-hand limit $\lim_{x \to 0^-} f(x)$ does not exist.

Now let's analyze $h(x) = |g(f(x))|$ around $x=0$. The domain of $h(x)$ is the same as the domain of $f(x)$, which is $\mathbb{R} \setminus [-1, 0)$.

Evaluate $h(x)$ at $x=0$: $h(0) = |g(f(0))| = |g(0)|$. $g(0) = 2\tan^{-1}|0| - \frac{\pi}{2} = 2\tan^{-1}(0) - \frac{\pi}{2} = 2(0) - \frac{\pi}{2} = -\frac{\pi}{2}$. $h(0) = |-\frac{\pi}{2}| = \frac{\pi}{2}$.

Evaluate the right-hand limit of $h(x)$ as $x \to 0^+$: $\lim_{x \to 0^+} h(x) = \lim_{x \to 0^+} |g(f(x))|$. As $x \to 0^+$, $f(x) \to 0$. Specifically, for $x \in (0, \epsilon)$, $f(x) = 0$. So, $\lim_{x \to 0^+} h(x) = |g(\lim_{x \to 0^+} f(x))| = |g(0)| = |-\frac{\pi}{2}| = \frac{\pi}{2}$. Alternatively, for $x \in (0, \epsilon)$, $h(x) = |g(0)| = \frac{\pi}{2}$. So $\lim_{x \to 0^+} h(x) = \frac{\pi}{2}$.

Evaluate the left-hand limit of $h(x)$ as $x \to 0^-$: $\lim_{x \to 0^-} h(x) = \lim_{x \to 0^-} |g(f(x))|$. Since $f(x)$ is undefined for $x \in [-1, 0)$, $g(f(x))$ and hence $h(x)$ are undefined for $x$ in any left neighborhood of 0. Therefore, the left-hand limit $\lim_{x \to 0^-} h(x)$ does not exist.

For $h(x)$ to be continuous at $x=0$, the limit $\lim_{x \to 0} h(x)$ must exist and be equal to $h(0)$. The limit $\lim_{x \to 0} h(x)$ exists if and only if the left-hand limit and the right-hand limit exist and are equal. We have $\lim_{x \to 0^+} h(x) = \frac{\pi}{2}$, but $\lim_{x \to 0^-} h(x)$ does not exist. Since the left-hand limit does not exist, the limit $\lim_{x \to 0} h(x)$ does not exist. Thus, $h(x)$ is discontinuous at $x=0$.

Let's check the options: (A) h is continuous at x = 0. False. (B) h is discontinuous at x = 0. True. (C) h (0-) = $\pi/2$. This means $\lim_{x \to 0^-} h(x) = \pi/2$. False, the limit does not exist. (D) h(0+) = –$\pi/2$. This means $\lim_{x \to 0^+} h(x) = -\pi/2$. False, the limit is $\pi/2$.

The only correct statement is that $h$ is discontinuous at $x=0$.