Question

Let a>0, d>0. Find the value of determinant

$\begin{vmatrix} \frac{1}{a} & \frac{1}{(a + d)} & \frac{1}{(a + 2d)}\\ \frac{1}{(a + d)} & \frac{1}{(a + 2d)} & \frac{1}{(a + 3d)}\\ \frac{1}{(a + 2d)} & \frac{1}{(a + 3d)} & \frac{1}{(a + 4d)} \end{vmatrix}$

Answer 1

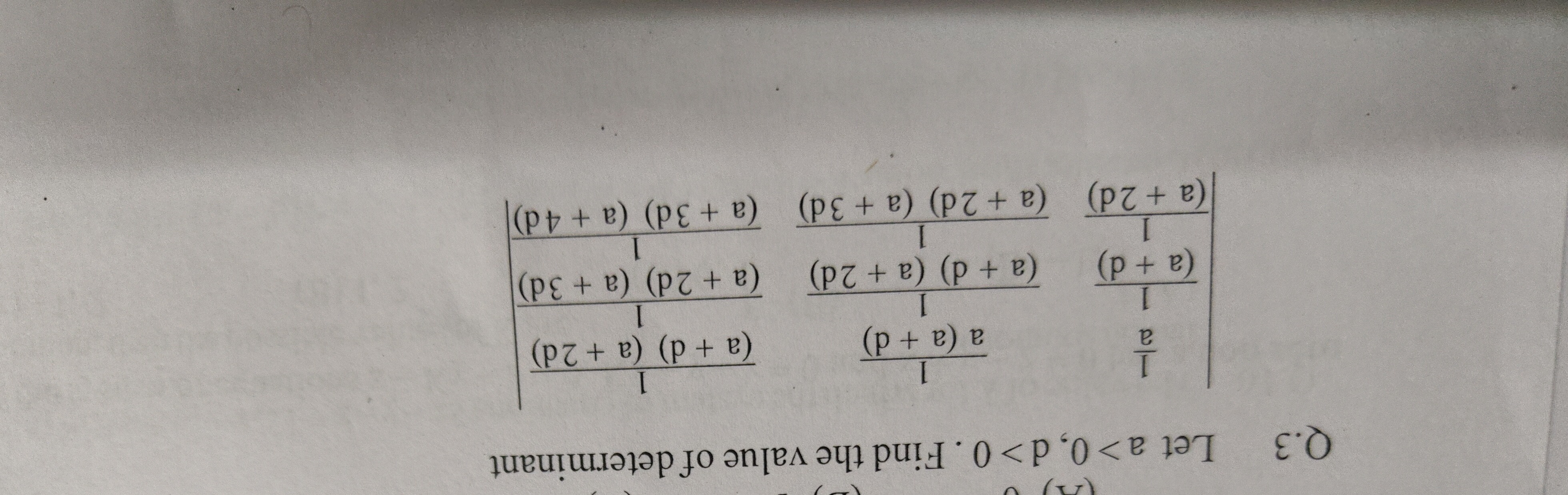
$\frac{4d^6}{a(a+d)^2(a+2d)^3(a+3d)^2(a+4d)}$

Answer 2

Let the given determinant be $\Delta$.

$$\Delta = \begin{vmatrix} \frac{1}{a} & \frac{1}{(a + d)} & \frac{1}{(a + 2d)}\\ \frac{1}{(a + d)} & \frac{1}{(a + 2d)} & \frac{1}{(a + 3d)}\\ \frac{1}{(a + 2d)} & \frac{1}{(a + 3d)} & \frac{1}{(a + 4d)} \end{vmatrix}$$

Apply the column operations $C_2 \to C_2 - C_1$ and $C_3 \to C_3 - C_2$.

$$\Delta = \begin{vmatrix} \frac{1}{a} & \frac{-d}{a(a+d)} & \frac{-d}{(a+d)(a+2d)}\\ \frac{1}{a+d} & \frac{-d}{(a+d)(a+2d)} & \frac{-d}{(a+2d)(a+3d)}\\ \frac{1}{a+2d} & \frac{-d}{(a+2d)(a+3d)} & \frac{-d}{(a+3d)(a+4d)} \end{vmatrix}$$

Take out common factors $(-d)$ from $C_2$ and $C_3$:

$$\Delta = (-d)^2 \begin{vmatrix} \frac{1}{a} & \frac{1}{a(a+d)} & \frac{1}{(a+d)(a+2d)}\\ \frac{1}{a+d} & \frac{1}{(a+d)(a+2d)} & \frac{1}{(a+2d)(a+3d)}\\ \frac{1}{a+2d} & \frac{1}{(a+2d)(a+3d)} & \frac{1}{(a+3d)(a+4d)} \end{vmatrix}$$

Apply row operations $R_2 \to R_2 - R_1$ and $R_3 \to R_3 - R_2$:

$$\Delta = d^2 \begin{vmatrix} \frac{1}{a} & \frac{1}{a(a+d)} & \frac{1}{(a+d)(a+2d)}\\ \frac{-d}{a(a+d)} & \frac{-2d}{a(a+d)(a+2d)} & \frac{-2d}{(a+d)(a+2d)(a+3d)}\\ \frac{-d}{(a+d)(a+2d)} & \frac{-2d}{(a+d)(a+2d)(a+3d)} & \frac{-2d}{(a+2d)(a+3d)(a+4d)} \end{vmatrix}$$

Take out common factors $(-d)$ from $R_2$ and $R_3$:

$$\Delta = d^2 (-d)^2 \begin{vmatrix} \frac{1}{a} & \frac{1}{a(a+d)} & \frac{1}{(a+d)(a+2d)}\\ \frac{1}{a(a+d)} & \frac{2}{a(a+d)(a+2d)} & \frac{2}{(a+d)(a+2d)(a+3d)}\\ \frac{1}{(a+d)(a+2d)} & \frac{2}{(a+d)(a+2d)(a+3d)} & \frac{2}{(a+2d)(a+3d)(a+4d)} \end{vmatrix}$$

Take out common factors from columns: $\frac{1}{a}$ from $C_1$, $\frac{1}{a+d}$ from $C_2$, $\frac{1}{(a+2d)}$ from $C_3$.

The common factors are: $\frac{1}{a}$, $\frac{1}{a+d}$, $\frac{1}{a+2d}$ from $R_1, R_2, R_3$ respectively. And $\frac{1}{a}$, $\frac{1}{a+d}$, $\frac{1}{a+2d}$ from $C_1, C_2, C_3$ respectively is incorrect.

Let's restart from the $R_2 \to R_2 - R_1$ and $R_3 \to R_3 - R_1$ step.

$$\Delta = \begin{vmatrix} \frac{1}{a} & \frac{1}{a+d} & \frac{1}{a+2d}\\ \frac{1}{a+d} & \frac{1}{a+2d} & \frac{1}{a+3d}\\ \frac{1}{a+2d} & \frac{1}{a+3d} & \frac{1}{a+4d} \end{vmatrix}$$

Apply $R_2 \to R_2 - R_1$ and $R_3 \to R_3 - R_1$:

$$\Delta = \begin{vmatrix} \frac{1}{a} & \frac{1}{a+d} & \frac{1}{a+2d}\\ \frac{-d}{a(a+d)} & \frac{-d}{(a+d)(a+2d)} & \frac{-d}{(a+2d)(a+3d)}\\ \frac{-2d}{a(a+2d)} & \frac{-2d}{(a+d)(a+3d)} & \frac{-2d}{(a+2d)(a+4d)} \end{vmatrix}$$

Take out $(-d)$ from $R_2$ and $(-2d)$ from $R_3$:

$$\Delta = (-d)(-2d) \begin{vmatrix} \frac{1}{a} & \frac{1}{a+d} & \frac{1}{a+2d}\\ \frac{1}{a(a+d)} & \frac{1}{(a+d)(a+2d)} & \frac{1}{(a+2d)(a+3d)}\\ \frac{1}{a(a+2d)} & \frac{1}{(a+d)(a+3d)} & \frac{1}{(a+2d)(a+4d)} \end{vmatrix}$$ $$\Delta = 2d^2 \begin{vmatrix} \frac{1}{a} & \frac{1}{a+d} & \frac{1}{a+2d}\\ \frac{1}{a(a+d)} & \frac{1}{(a+d)(a+2d)} & \frac{1}{(a+2d)(a+3d)}\\ \frac{1}{a(a+2d)} & \frac{1}{(a+d)(a+3d)} & \frac{1}{(a+2d)(a+4d)} \end{vmatrix}$$

Take out common factors from columns: $\frac{1}{a}$ from $C_1$, $\frac{1}{a+d}$ from $C_2$, $\frac{1}{a+2d}$ from $C_3$:

$$\Delta = 2d^2 \cdot \frac{1}{a} \cdot \frac{1}{a+d} \cdot \frac{1}{a+2d} \begin{vmatrix} 1 & 1 & 1\\ \frac{1}{a+d} & \frac{1}{a+2d} & \frac{1}{a+3d}\\ \frac{1}{a+2d} & \frac{1}{a+3d} & \frac{1}{a+4d} \end{vmatrix}$$

Let $D' = \begin{vmatrix} 1 & 1 & 1\\ \frac{1}{a+d} & \frac{1}{a+2d} & \frac{1}{a+3d}\\ \frac{1}{a+2d} & \frac{1}{a+3d} & \frac{1}{a+4d} \end{vmatrix}$.

Apply $C_2 \to C_2 - C_1$ and $C_3 \to C_3 - C_1$:

$$D' = \begin{vmatrix} 1 & 0 & 0\\ \frac{1}{a+d} & \frac{1}{a+2d} - \frac{1}{a+d} & \frac{1}{a+3d} - \frac{1}{a+d}\\ \frac{1}{a+2d} & \frac{1}{a+3d} - \frac{1}{a+2d} & \frac{1}{a+4d} - \frac{1}{a+2d} \end{vmatrix}$$

Expand along $R_1$:

$$D' = \begin{vmatrix} \frac{-d}{(a+d)(a+2d)} & \frac{-2d}{(a+d)(a+3d)}\\ \frac{-d}{(a+2d)(a+3d)} & \frac{-2d}{(a+2d)(a+4d)} \end{vmatrix}$$

Take out $(-d)$ from $C_1$ and $(-2d)$ from $C_2$:

$$D' = (-d)(-2d) \begin{vmatrix} \frac{1}{(a+d)(a+2d)} & \frac{1}{(a+d)(a+3d)}\\ \frac{1}{(a+2d)(a+3d)} & \frac{1}{(a+2d)(a+4d)} \end{vmatrix}$$ $$D' = 2d^2 \left[ \frac{1}{(a+d)(a+2d)} \cdot \frac{1}{(a+2d)(a+4d)} - \frac{1}{(a+d)(a+3d)} \cdot \frac{1}{(a+2d)(a+3d)} \right]$$ $$D' = 2d^2 \left[ \frac{1}{(a+d)(a+2d)^2(a+4d)} - \frac{1}{(a+d)(a+2d)(a+3d)^2} \right]$$ $$D' = \frac{2d^2}{(a+d)(a+2d)} \left[ \frac{1}{(a+2d)(a+4d)} - \frac{1}{(a+3d)^2} \right]$$ $$D' = \frac{2d^2}{(a+d)(a+2d)} \left[ \frac{(a+3d)^2 - (a+2d)(a+4d)}{(a+2d)(a+4d)(a+3d)^2} \right]$$

The numerator of the bracket term is: $(a+3d)^2 - (a+2d)(a+4d) = (a^2 + 6ad + 9d^2) - (a^2 + 4ad + 2ad + 8d^2)$ $= a^2 + 6ad + 9d^2 - a^2 - 6ad - 8d^2 = d^2$

So,

$$D' = \frac{2d^2}{(a+d)(a+2d)} \left[ \frac{d^2}{(a+2d)(a+4d)(a+3d)^2} \right] = \frac{2d^4}{(a+d)(a+2d)^2(a+3d)^2(a+4d)}$$

Substitute $D'$ back into the expression for $\Delta$:

$$\Delta = 2d^2 \cdot \frac{1}{a(a+d)(a+2d)} \cdot \frac{2d^4}{(a+d)(a+2d)^2(a+3d)^2(a+4d)}$$ $$\Delta = \frac{4d^6}{a(a+d)^2(a+2d)^3(a+3d)^2(a+4d)}$$

The final answer is $\boxed{\frac{4d^6}{a(a+d)^2(a+2d)^3(a+3d)^2(a+4d)}}$.