Question

In which of the following cases there does not exist any function -

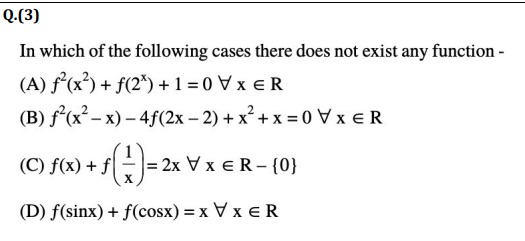
• A. $f^2(x^2) + f(2^x) + 1 = 0 \quad \forall x \in R$
• B. $f^2(x^2-x) - 4f(2x-2) + x^2 + x = 0 \quad \forall x \in R$
• C. $f(x) + f(\frac{1}{x}) = 2x \quad \forall x \in R - \{0\}$
• D. $f(sinx) + f(cosx) = x \quad \forall x \in R$

Answer 1

Answer: (A), (C), (D)

A, C, D

Answer 2

Let's analyze each option to determine if a function $f: R \to R$ satisfying the given equation exists.

(A) $f^2(x^2) + f(2^x) + 1 = 0 \quad \forall x \in R$

Let $x=2$. The equation becomes $f^2(2^2) + f(2^2) + 1 = 0$, which simplifies to $f^2(4) + f(4) + 1 = 0$. Let $y = f(4)$. The equation is $y^2 + y + 1 = 0$. This is a quadratic equation for $y$. The discriminant is $\Delta = 1^2 - 4(1)(1) = 1 - 4 = -3$. Since the discriminant is negative, the quadratic equation $y^2 + y + 1 = 0$ has no real solutions for $y$. However, if a function $f: R \to R$ exists, then $f(4)$ must be a real number. Since there is no real number $y$ such that $y^2 + y + 1 = 0$, there is no real number $f(4)$ that can satisfy the equation when $x=2$. Therefore, there does not exist any function $f: R \to R$ satisfying the given equation for all $x \in R$.

(C) $f(x) + f(\frac{1}{x}) = 2x \quad \forall x \in R - \{0\}$

Replacing $x$ with $1/x$ gives $f(1/x) + f(x) = 2/x$. Equating the right sides gives $2x = 2/x$, or $x^2=1$, which means $x = \pm 1$. But the original equation is for all $x \in R - \{0\}$. This is a contradiction. Thus, no such function exists.

(D) $f(\sin x) + f(\cos x) = x \quad \forall x \in R$

Setting $x=0$ gives $f(\sin 0) + f(\cos 0) = 0$, so $f(0)+f(1)=0$. Setting $x=\pi/2$ gives $f(\sin \pi/2) + f(\cos \pi/2) = \pi/2$, so $f(1)+f(0)=\pi/2$. Thus $0=\pi/2$, a contradiction. Thus, no such function exists.

Therefore, options (A), (C), and (D) do not have any function satisfying the given equation.