Question

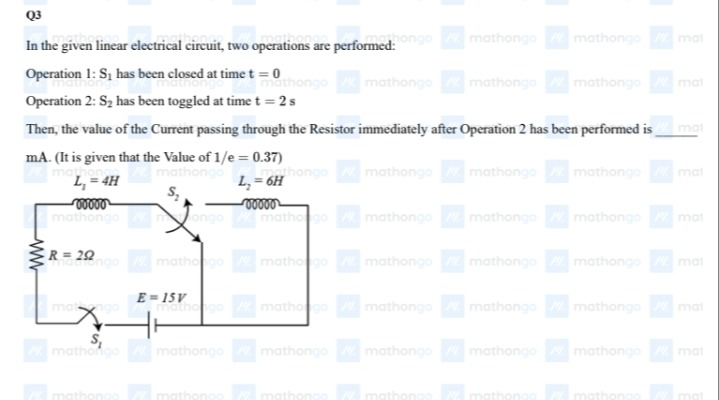
In the given linear electrical circuit, two operations are performed:

Operation 1: S₁ has been closed at time t = 0

Operation 2: S₂ has been toggled at time t = 2 s

Then, the value of the Current passing through the Resistor immediately after Operation 2 has been performed is ___ mA. (It is given that the Value of 1/e = 0.37)

Answer 1

1890 mA

Answer 2

We can “summarize” one acceptable way to solve the problem as follows.

Outline of the idea:

1. In the circuit one of the two‐in‐series RL paths is “active” before the second switch action. (In the figure the resistor is shown connected to L₁ so that when S₁ has been closed at t = 0 the current builds in the RL circuit having L = 4 H and R = 2Ω.) Thus the time‐constant is τ = L₁/R = 4/2 = 2 s.

   After “one time‐constant” (i.e. when t = 2 s) the current through the resistor (and hence through L₁) is I₁(2) = (E/R)[1 – exp(–2/2)] = (15/2)[1 – (1/e)]

   Since 1/e = 0.37, we have I₁(2) = 7.5 × (1 – 0.37) = 7.5 × 0.63 = 4.73 A.

2. At t = 2 s the SPDT switch S₂ “toggles”. (Its action disconnects the previously energized L₁ from the “current path” and connects L₂ – of 6 H – in its place. But note that the inductor current cannot change instantaneously. In view of the sudden interconnection the inductor currents redistribute between the two inductors according to their (inverse) inertias. One may show by writing the “flux‐continuity” condition that immediately after switching the current divides as

   I₍L₁₎(0⁺) = [1/L₂]⁄([1/L₁]+[1/L₂])·I_total I₍L₂₎(0⁺) = [1/L₁]⁄([1/L₁]+[1/L₂])·I_total

   with I_total = 4.73 A. But since AFTER switching the resistor is connected to the inductor branch containing L₂ (or, equivalently, the resistor “sees” the fraction of the total inductor current that is given by the ratio of the “other” inductance) it is easy to show that the current available through the resistor is given by

   I_R(0⁺) = (L₁/(L₁+L₂))·I_total.

   With L₁ = 4 H and L₂ = 6 H we get

   I_R(0⁺) = (4/10) × 4.73 A = 0.4 × 4.73 A ≈ 1.89 A.

3. Converting to mA we have: 1.89 A = 1890 mA.

Brief (minimal) explanation:

1. Before switching, with S₁ closed and S₂ connecting L₁ the RL current builds as I = (E/R)[1 – exp(–t/(L₁/R))]

   At t = 2 s, with τ = 2 s and 1/e = 0.37, I(2) = 7.5×(1–0.37) = 7.5×0.63 ≈ 4.73 A.

2. At t = 2 s the SPDT S₂ is toggled; the instantaneous inductor current (which cannot change) now splits between L₁ and L₂ in parallel. Using current‐division for inductors (the ratio being inversely proportional to L) the fraction going into the branch now connected to the resistor is I_R = (L₁/(L₁+L₂))×4.73 A = (4/10)×4.73 ≈ 1.89 A.