Question

If $y=\tan^{-1}x+\cot^{-1}x+\sec^{-1}x$, then $y=$?

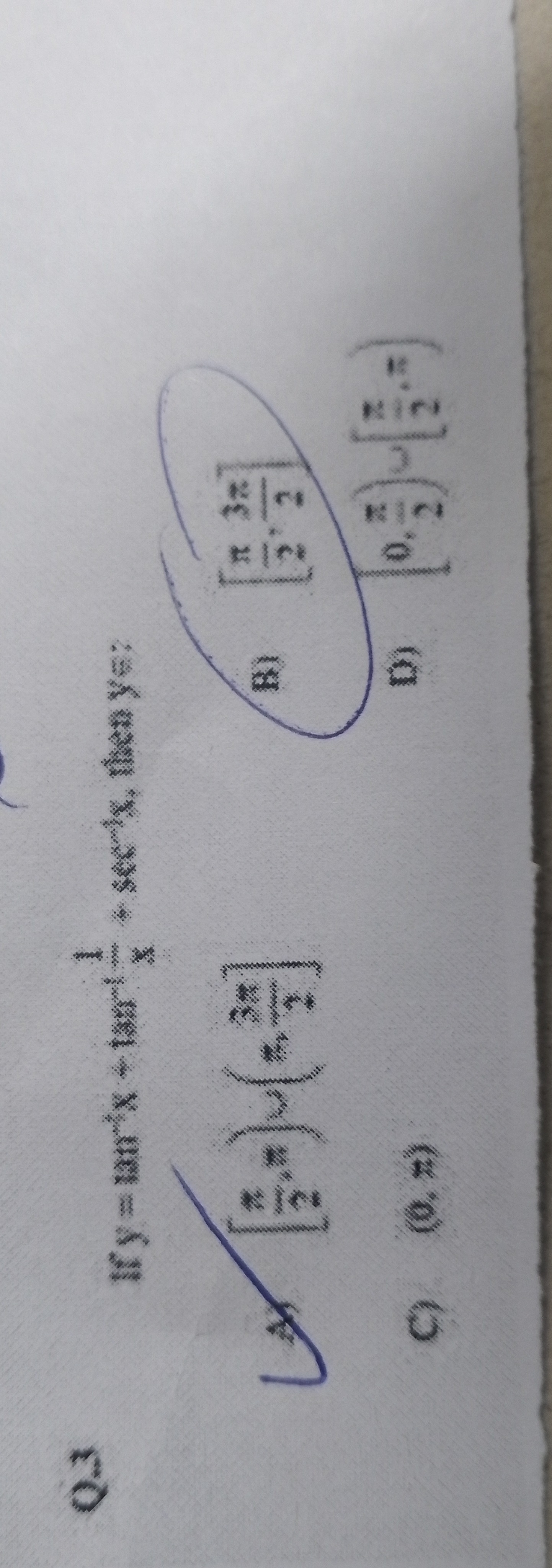
• A. $(0,x)$
• B. $\left[\frac{\pi}{2},\frac{3\pi}{2}\right]$
• C. $(0,x)$
• D. $\left[0,\frac{\pi}{2}\right]$

Answer 1

Answer: (B)

$\left[\frac{\pi}{2},\frac{3\pi}{2}\right]$

Answer 2

The function is $y=\tan^{-1}x+\cot^{-1}x+\sec^{-1}x$. The domain of the function is $(-\infty, -1] \cup [1, \infty)$. Using the identity $\tan^{-1}x+\cot^{-1}x = \frac{\pi}{2}$, the function simplifies to $y = \frac{\pi}{2} + \sec^{-1}x$ for $x$ in its domain. The range of $\sec^{-1}x$ for $x \in (-\infty, -1] \cup [1, \infty)$ is $[0, \frac{\pi}{2}) \cup (\frac{\pi}{2}, \pi]$. Adding $\frac{\pi}{2}$ to this range gives the range of $y$ as $[\frac{\pi}{2}, \pi) \cup (\pi, \frac{3\pi}{2}]$. This range is a subset of the interval $[\frac{\pi}{2}, \frac{3\pi}{2}]$. Among the given options, $[\frac{\pi}{2}, \frac{3\pi}{2}]$ is the interval that contains the range of $y$.